Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C.
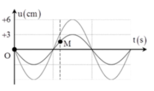
Tại thời điểm t 1 tốc độ của M là v M = ω A M 2
Tốc độ của điểm N tịa thời điểm t 2 là:
v N = ω A N 2 2
v N = v M ⇒ A N = 2 2 A M
Vậy điểm này cách nút λ 8 ⇒ x N = 15 c m
Dựa vào hình vẽ u N = 2 2 A N = A M 2 = 2 c m

Đáp án A
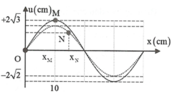
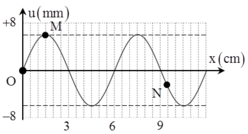
+ Từ đồ thị, ta thấy rằng điểm M dao động với biên độ bằng một nửa biên độ bụng A M = 3 c m
+ Khi hình ảnh sợi dây là đường liền nét, ta xét một điểm bụng có li độ u = 3 cm=0,5Ab → khoảng thời gian ngắn nhất để điểm bụng này quay lại li độ này sẽ là
![]()
+ Điểm M tại thời điểm t 1 đang ở vị trí biên, thời điểm t 2 = t 1 + 1 15 s tương ứng với góc quét ∆ φ = ω ∆ t = 2 π 3
tại
t
2
M có li độ 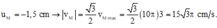

+ Ta thấy M và N thuộc hai bó sóng đối xứng với nhau qua nút nên luôn dao động ngược pha nhau.
Mặc khác dựa vào độ chia nhỏ nhất của trục Ox, ta thấy rằng N cách nút gần nhất một đoạn λ 12 do đó sẽ dao động với biên độ bằng một nửa biên độ điểm bụng M.
+ Với hai đại lượng ngược pha ta luôn có:
v N v M = ω A N ω A M ⇒ v M = - 0 , 5 v M = - 4 π cm/s li đô tương ứng của điểm N khi đó
u N = - A N 2 - v N ω 2 = - 0 , 4 2 - - 4 π 2 π . 10 2 = - 3 5 mm
Gia tốc của điểm N:
a N = - ω 2 x N = - ( 2 π . 10 ) 2 - 3 5 = 8 3 m / s 2
Đáp án C

O u 3 a t M 2a
Điều kiện sóng dừng 2 đầu cố định: \(l=\frac{k\lambda}{2}\Rightarrow\lambda=l=\frac{v}{f}\Rightarrow f=\frac{v}{l}\)(Với k = 2, vì trên hình có 2 bụng).
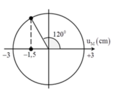
Thời gian từ \(u=x\rightarrow u=-x\) (liên tiếp): \(5\Delta t-\Delta t=4\Delta t\)
Suy ra thời gian từ vị trí: \(u=x\rightarrow u=0\) là: \(\frac{4\Delta t}{2}=2\Delta t\)
Suy ra thời gian đi từ vị trí: \(u=2a\rightarrow u=0\) (biên về VTCB) là \(\Delta t+2\Delta t=3\Delta t=\frac{T}{4}\)
Chu kì dao động: \(T=4.3\Delta t=12\Delta t\)
Suy ra: \(A_M=x=2a.\frac{\sqrt{3}}{2}=a\sqrt{3}\) (dựa vào hình vẽ, cung \(\Delta t\) ứng với 300).
Dựa vào vòng tròn: \(V_M\) \(_{max}=a\sqrt{3}.\omega=a\sqrt{3}.2\pi f=2\pi\sqrt{3}\frac{va}{l}\)
Đáp án B

Chọn đáp án B
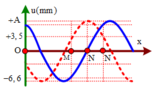
Từ đồ thị ta thấy rằng hai thời điểm t 1 v à t 2 vuông pha nhau, do vậy
Δ t = 0 , 5 = 2 k + 1 T 4 ⇒ ω = 2 k + 1 π r a d / s
Tại thời điểm t 1 điểm N đang đi qua vị trí cân bằng theo chiều âm do vậy tốc độ của N sẽ là: v N 1 = v max = ω A = 7 , 5 π 2 k + 1 m m / s
Vận tốc của N tại thời điểm t 0 = t 1 − 1 9 s : v N 0 = − v N 1 cos 2 k + 1 π 9 m m / s (mm/s)
Với k = 1, ta thu được vN = -3,53 cm/s

Ta có $\lambda =24cm $
Bạn vẽ hình ra .
Đoạn AB =24cm sau đó vẽ 2 bụng sóng.
Lấy M N nằm giữa sao cho MN= AB/3 = 8 cm.
Khoảng cách MN lớn nhất khi chúng nằm trên bụng và nhỏ nhất khi duỗi thẳng.
Ta có $\dfrac{MN_{lớn}}{MN_{nhỏ}} =1.25 \rightarrow MN_{lớn}=10 \rightarrow $biên độ của M và N là 3cm.
Khoảng cách từ M đến nút bằng 4cm =$\dfrac{\lambda}{6} \rightarrow A_{bụng} =2\sqrt{3}$

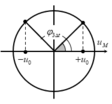
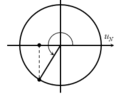
+ Xét một điểm N trên dây là bụng sóng, ta biểu diễn dao động của phần tử này tương ứng trên đường tròn.

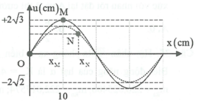

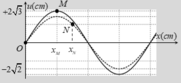


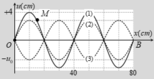
Tại thời điểm t 1 tốc độ của M là v M = ω A M 2
Tốc độ của điểm N tịa thời điểm t 2 là:
v N = ω A N 2 2
v N = v M ⇒ A N = 2 2 A M
Vậy điểm này cách nút λ 8 ⇒ x N = 15 c m
Dựa vào hình vẽ u N = 2 2 A N = A M 2 = 2 c m
Chọn đáp án C