Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi số học sinh nam là x \(\Rightarrow\) nữ là \(30-x\) (\(2\le x< 30\))
Không gian mẫu: \(C_{30}^3\)
Số cách chọn ra 2 nam và 1 nữ: \(C_x^2.C_{30-x}^1\)
Xác suất: \(\frac{C_x^2C_{30-x}^1}{C_{30}^3}=\frac{12}{29}\)
\(\Rightarrow x=16\)
Vậy có 16 nam và 14 nữ
c/
\(\Leftrightarrow\frac{1}{2}cosx-\frac{\sqrt{3}}{2}sinx=cos3x\)
\(\Leftrightarrow cos\left(x+\frac{\pi}{3}\right)=cos3x\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{\pi}{3}=3x+k2\pi\\x+\frac{\pi}{3}=-3x+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k\pi\\x=\frac{\pi}{12}+\frac{k\pi}{2}\end{matrix}\right.\)
d/
\(\Leftrightarrow\frac{1}{2}sin3x-\frac{\sqrt{3}}{2}cos3x=sin2x\)
\(\Leftrightarrow sin\left(3x-\frac{\pi}{3}\right)=sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\frac{\pi}{3}=2x+k2\pi\\3x-\frac{\pi}{3}=\pi-2x+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}+k2\pi\\x=\frac{4\pi}{15}+\frac{k2\pi}{5}\end{matrix}\right.\)
a/
\(\Leftrightarrow\frac{1}{2}sinx+\frac{\sqrt{3}}{2}cosx=sin\left(x+\frac{\pi}{6}\right)\)
\(\Leftrightarrow sin\left(x+\frac{\pi}{3}\right)=sin\left(x+\frac{\pi}{6}\right)\)
\(\Rightarrow x+\frac{\pi}{3}=\pi-x-\frac{\pi}{6}+k2\pi\)
\(\Rightarrow x=\frac{\pi}{4}+k\pi\)
b/
\(\Leftrightarrow\frac{\sqrt{3}}{2}sinx+\frac{1}{2}cosx=sin\frac{\pi}{12}\)
\(\Leftrightarrow sin\left(x+\frac{\pi}{6}\right)=sin\frac{\pi}{12}\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{\pi}{6}=\frac{\pi}{12}+k2\pi\\x+\frac{\pi}{6}=\frac{11\pi}{12}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{12}+k2\pi\\x=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)
a) cosx - √3sinx = √2 ⇔ cosx - tan
sinx = √2
⇔ coscosx - sinsinx = √2cos ⇔ cos(x + ) = 
⇔ 
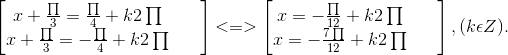
b) 3sin3x - 4cos3x = 5 ⇔ 
sin3x - 
cos3x = 1.
Đặt α = arccos thì phương trình trở thành
cosαsin3x - sinαcos3x = 1 ⇔ sin(3x - α) = 1 ⇔ 3x - α = 
+ k2π
⇔ x = 
, k ∈ Z (trong đó α = arccos).
\(K=\lim\limits n\left(\sqrt[3]{1+\frac{1}{n}-\frac{1}{n^3}}-1+3\left(2-\sqrt{4+\frac{1}{n}+\frac{1}{n^2}}\right)\right)\)
\(=\lim\limits n\left[\frac{\frac{1}{n}-\frac{1}{n^3}}{\sqrt[3]{\left(1+\frac{1}{n}-\frac{1}{n^3}\right)^2}+\sqrt[3]{1+\frac{1}{n}-\frac{1}{n^3}}+1}-\frac{3\left(\frac{1}{n}+\frac{1}{n^2}\right)}{2+\sqrt{4+\frac{1}{n}+\frac{1}{n^2}}}\right]\)
\(=\lim\limits\left[\frac{1-\frac{1}{n^2}}{\sqrt[3]{\left(1+\frac{1}{n}-\frac{1}{n^3}\right)^2}+\sqrt[3]{1+\frac{1}{n}-\frac{1}{n^3}}+1}-\frac{3\left(1+\frac{1}{n}\right)}{2+\sqrt{4+\frac{1}{n}+\frac{1}{n^2}}}\right]\)
\(=\frac{1}{1+1+1}-\frac{3}{2+2}=-\frac{5}{12}\)
S A B C D H M N K
Kẻ \(AH\perp BD\Rightarrow BD\perp\left(SAH\right)\Rightarrow\widehat{SHA}\) là góc giữa (SBD) và (ABCD)
\(\frac{1}{AH^2}=\frac{1}{AD^2}+\frac{1}{AB^2}\Rightarrow AH=\frac{AB.AD}{\sqrt{AB^2+AD^2}}=\frac{a\sqrt{3}}{2}\)
\(SA=\sqrt{SD^2-AD^2}=2a\)
\(tan\widehat{SHA}=\frac{SA}{AH}=\frac{4\sqrt{3}}{3}\Rightarrow\widehat{SHA}\simeq66^035'\)
b/ \(MS=MA\Rightarrow d\left(S;\left(MND\right)\right)=d\left(A;\left(MND\right)\right)\)
Từ A kẻ \(AK\perp MD\Rightarrow AK\perp\left(MND\right)\Rightarrow AK=d\left(A;\left(MND\right)\right)\)
\(AM=\frac{SA}{2}=a\Rightarrow\frac{1}{AK^2}=\frac{1}{AM^2}+\frac{1}{AD^2}\Rightarrow AK=\frac{AM.AD}{\sqrt{AM^2+AD^2}}=\frac{a\sqrt{3}}{2}\)
ĐKXĐ: ...
\(\Leftrightarrow\frac{3cos^2x}{sin^2x}-2cosx+2\sqrt{2}sin^2x-3\sqrt{2}cosx=0\)
\(\Leftrightarrow cosx\left(\frac{3cosx-2sin^2x}{sin^2x}\right)-\sqrt{2}\left(3cosx-2sin^2x\right)=0\)
\(\Leftrightarrow\left(3cosx-2sin^2x\right)\left(\frac{cosx}{sin^2x}-\sqrt{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3cosx-2sin^2x=0\\cosx-\sqrt{2}sin^2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2cos^2x+3cosx-2=0\\\sqrt{2}cos^2x+cosx-\sqrt{2}=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}cosx=\frac{1}{2}\\cosx=\frac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}+k2\pi\\x=\frac{\pi}{4}+k2\pi\end{matrix}\right.\) \(\Rightarrow\alpha.\beta=\frac{\pi^2}{12}\)
Chọn C
Số cách chọn 3 người từ một nhóm 12 người là: C 12 3