Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số tập hợp con có k phần tử của tập hợp A (có 18 phần tử)
\(C_{18}^k\left(k=1,.....,18\right)\)
Để tìm max \(C_{18}^k,k\in\left\{1,2,.....,18\right\}\) (*), ta tiến hành giải bất phương trình sau :
\(\frac{C_{18}^k}{C_{18}^{k+1}}< 1\)
\(\Leftrightarrow C_{18}^k< C_{18}^{k+1}\)
\(\Leftrightarrow\frac{18!}{\left(18-k\right)!k!}< \frac{18!}{\left(17-k\right)!\left(k+1\right)!}\)
\(\Leftrightarrow\left(18-k\right)!k!>\left(17-k\right)!\left(k+1\right)!\)
\(\Leftrightarrow17>2k\)
\(\Leftrightarrow k< \frac{17}{2}\)
Điều kiện (*) nên k = 1,2,3,.....8
Suy ra \(\frac{C_{18}^k}{C_{18}^{k+1}}>1\) khi k = 9,10,...,17
Vậy ta có
\(C^1_{18}< C_{18}^2< C_{18}^3< .........C_{18}^8< C_{18}^9>C_{18}^{10}>.....>C_{18}^{18}\)
Vậy \(C_{18}^k\) đạt giá trị lớn nhất khi k = 9. Như thế số tập hợp con gồm 9 phần tử của A là số tập hợp con lớn nhất.

ta có : \(Q=C^1_n+2\dfrac{C_n^2}{C_n^1}+...+k\dfrac{C^k_n}{C_n^{k-1}}+...+n\dfrac{C^n_n}{C_n^{n-1}}\)
\(\Leftrightarrow Q=\dfrac{n!}{1!\left(n-1\right)!}+2\dfrac{1!\left(n-1\right)!}{2!\left(n-2\right)!}+...+k\dfrac{\left(k-1\right)!\left(n-k+1\right)!}{k!\left(n-k\right)!}+...+\dfrac{n\left(n-1\right)!1!}{n!}\)
\(\Leftrightarrow Q=n+\dfrac{2\left(n-1\right)}{2}+...+\dfrac{k\left(n-k+1\right)}{k}+...+\dfrac{n}{n}\)
\(\Leftrightarrow Q=n+\left(n-1\right)+...+\left(n-k+1\right)+...+1\)
\(\Leftrightarrow Q=n^2-\left(1+\left(1+1\right)+\left(1+2\right)+...+\left(n-1\right)\right)\)

1/ \(2C^k_n+5C^{k+1}_n+4C^{k+2}_n+C^{k+3}_n\)
\(=2\left(C^k_n+C_n^{k+1}\right)+3\left(C^{k+1}_n+C^{k+2}_n\right)+\left(C^{k+2}_n+C^{k+3}_n\right)\)
\(=2C_{n+1}^{k+1}+3C_{n+1}^{k+2}+C_{n+1}^{k+3}\)
\(=2\left(C_{n+1}^{k+1}+C_{n+1}^{k+2}\right)+\left(C_{n+1}^{k+2}+C^{k+3}_{n+1}\right)\)
\(=2C_{n+2}^{k+2}+C_{n+2}^{k+3}=C_{n+2}^{k+2}+\left(C_{n+2}^{k+2}+C_{n+2}^{k+3}\right)=C_{n+2}^{k+2}+C_{n+3}^{k+3}\)
Áp dụng ct:C(k)(n)=C(k)(n-1)+C(k-1)(n-1) có:
................C(k-1)(n-1)= C(k)(n) - C(k)(n-1)
tương tự: C(k-1)(n-2)= C(k)(n-1) - C(k)(n-2)
................C(k-1)(n-3)= C(k)(n-2) -C(k)(n-3)
.........................................
................C(k-1)(k-1)= C(k)(k) (=1)
Cộng 2 vế vào với nhau...-> đpcm

Ta có :
\(C^{k+1}_{n+1}=C^k_n+C_n^{k+1}\)
\(C^{k+1}_n=C^k_{n-1}+C_{n-1}^{k+1}\)
...........
\(C^{k+1}_{k+2}=C^k_{k+1}+C_{k+1}^{k+1}\)
Từ đó :
\(C^{k+1}_{n+1}=C^k_n+C_{n-1}^k+....C^k_{k+1}+C^{k+1}_{k+1}\)
= \(C^k_n+C_{n-1}^k+....+C^k_{k+1}+C^k_k\)

Cho số tự nhiên n ≥ 4. Nếu \(C_n^4\) = K thì \(A^4_n\) bằng:
A. 24K
B. 4K
C. 16K
D. \(\frac{K}{24}\)
Chọn B
Do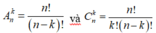 nên
C
n
k
=
A
n
k
k
!
.
nên
C
n
k
=
A
n
k
k
!
.