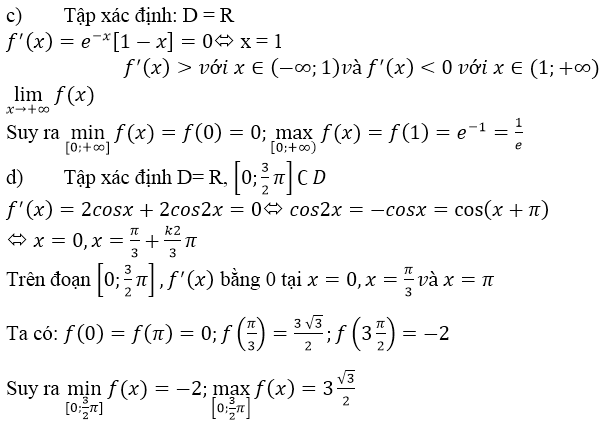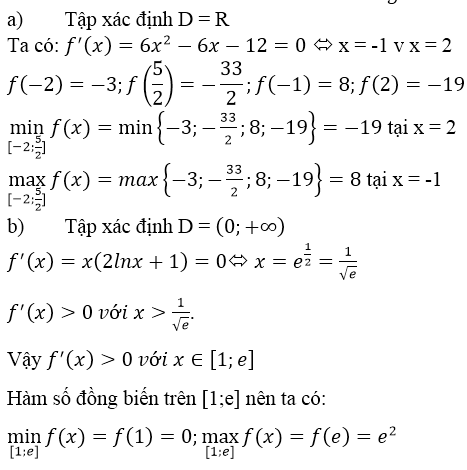Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tính E(300)=300/log2(300), E(90000)=90000/log2(90000)
Vì độ hiệu quả tỉ lệ thuận với thời gian thực hiện
nên ta có tỉ số 0,02/E(300)=x/E(90000) (x là giá trị cần tìm).
Từ đó tính được x=3

a) y = f(x) = x3 – 3mx2 + 3(2m-1)x + 1
Tập xác định: D = R
y’= 3x2 -6mx + 3(2m-1) = 3(x2 – 2mx + 2m – 1)
Hàm số đồng biến trên D = R ⇔ y’ ≥ 0, ∀x ∈ R
⇔ x2 – 2mx + 2m - 1≥0, ∀x ∈ R
⇔ Δ’ = m2 – 2m + 1 = (m-1)2 ≤ 0 ⇔ m =1
b) Hàm số có một cực đại và một cực tiểu
⇔ phương trình y’= 0 có hai nghiệm phân biệt
⇔ (m-1)2 > 0 ⇔ m≠1
c) f’’(x) = 6x – 6m > 6x
⇔ -6m > 0 ⇔ m < 0

Cứ tăng giá thêm 100.000 ngàn đồng/tháng thì có 2 căn bỏ trống
--> Tăng thêm 100.000*n ngàn đồng/tháng thì sẽ có 2n căn bị bỏ trống
Gọi x = 2*10^{6} + 10^{5}*n là giá cho thuê để được thu nhập cao nhất
Suy ra thu nhập là y = x*(50 - 2n) (vì trong 50 căn đã có 2n căn bị bỏ trống)
y = x(50 - 2n) = (2*10^{6} + 10^{5}*n) (50 - 2n) = -2*10^{5}*n^{2} + 10^{6}*n + 10^{8}
= -2*10^{5} (n^{2} - 5n - 500) = -2*10^{5} [(n - 5/2)^{2} - 506,25] = -2*10^{5}(n - 5/2)^{2} + 1.0125 * 10^{8}
Thấy y đạt giá trị lớn nhất bằng 1.0125*10^{8} khi n = 2,5
Vậy giá thuê để đạt thu nhập lớn nhất là x = 2.000.000 + 100.000*2,5 = 2.250.000 đồng/tháng

a) y= -x4 + 2mx2 – 2m + 1(Cm). Tập xác định: D = R
y ‘ = -4x3 + 4mx = -4x (x2 – m)
- Với m ≤ 0 thì y’ có một nghiệm x = 0 và đổi dấu + sang – khi qua nghiệm này. Do đó hàm số có một cực đại là x = 0

Do đó, hàm số có 2 cực trị tại x = ± √m và có một cực tiểu tại x = 0
b) Phương trình -x4 + 2mx2 – 2m + 1 = 0 luôn có nghiệm x = ± 1 với mọi m nên (Cm) luôn cắt trục hoành.
c) Theo lời giải câu a, ta thấy ngay:
với m > 0 thì đồ thị (Cm) có cực đại và cực tiểu.

a) f(x) = 2x3 – 3x2 – 12x + 1 ⇒ f’(x) = 6x2 – 6x – 12
f’(x) = 0 ⇔ x ∈ {-1, 2}
So sánh các giá trị:
f(x) = -3; f(-1) = 8;
f(2) = -19, f(52)=−332f(52)=−332
Suy ra:
maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19
b) f(x) = x2 lnx ⇒ f’(x)= 2xlnx + x > 0, ∀ x ∈ [1, e] nên f(x) đồng biến.
Do đó:
maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0
c) f(x) = f(x) = xe-x ⇒ f’(x)= e-x – xe-x = (1 – x)e-x nên:
f’(x) = 0 ⇔ x = 1, f’(x) > 0, ∀x ∈ (0, 1) và f’(x) < 0, ∀x ∈ (1, +∞)
nên:
maxx∈[0,+∞)f(x)=f(1)=1emaxx∈[0,+∞)f(x)=f(1)=1e
Ngoài ra f(x) = xe-x > 0, ∀ x ∈ (0, +∞) và f(0) = 0 suy ra
maxx∈[0,+∞)f(x)=f(0)=0maxx∈[0,+∞)f(x)=f(0)=0
d) f(x) = 2sinx + sin2x ⇒ f’(x)= 2cosx + 2cos2x
f’(x) = 0 ⇔ cos 2x = -cosx ⇔ 2x = ± (π – x) + k2π
⇔ x∈{−π+k2π;π3+k2π3}x∈{−π+k2π;π3+k2π3}
Trong khoảng [0,3π2][0,3π2] , phương trình f’(x) = 0 chỉ có hai nghiệm là x1=π3;x2=πx1=π3;x2=π
So sánh bốn giá trị : f(0) = 0; f(π3)=3√32;f(π)=0;f(3π2)=−2f(π3)=332;f(π)=0;f(3π2)=−2
Suy ra:
maxx∈[0,3π2]f(x)=f(π3)=3√32minx∈[0,3π2]f(x)=f(3π2)=−2



 {
{ ) ∈ ∆ ⇔
) ∈ ∆ ⇔ 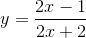 .
.