Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
\(6 = \sqrt {36} ; - 1,7 = - \sqrt {2,89} \)
Vì 0 < 2,89 < 3 nên 0> \( - \sqrt {2,89} > - \sqrt 3 \) hay 0 > -1,7 > \( - \sqrt 3 \)
Vì 0 < 35 < 36 < 47 nên \(0 < \sqrt {35} < \sqrt {36} < \sqrt {47} \) hay 0 < \(\sqrt {35} < 6 < \sqrt {47} \)
Vậy các số theo thứ tự tăng dần là: \( - \sqrt 3 ; - 1,7;0;\sqrt {35} ;6;\sqrt {47} \)
b) Ta có:
\(\sqrt {5\frac{1}{6}} = \sqrt {5,1(6)} ; - \sqrt {2\frac{1}{3}} = - \sqrt {2,(3)} \); -1,5 = \( - \sqrt {2,25} \)
Vì 0 < 2,25 < 2,3 < 2,(3) nên 0> \( - \sqrt {2,25} > - \sqrt {2,3} > - \sqrt {2,(3)} \) hay 0 > -1,5 > \( - \sqrt {2,3} > - \sqrt {2\frac{1}{3}} \)
Vì 5,3 > 5,1(6) > 0 nên \(\sqrt {5,3} > \sqrt {5,1(6)} \)> 0 hay \(\sqrt {5,3} > \sqrt {5\frac{1}{6}} > 0\)
Vậy các số theo thứ tự giảm dần là: \(\sqrt {5,3} ;\sqrt {5\frac{1}{6}} ;0\); -1,5; \( - \sqrt {2,3} ; - \sqrt {2\frac{1}{3}} \)

Lời giải:
Viết các phân số dưới dạng tối giản:
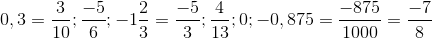
- So sánh các số hữu tỉ dương với nhau:
Ta có : 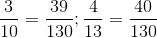
Vì 39 < 40 và 130 > 0 nên 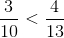
- Tương tự So sánh các số hữu tỉ âm với nhau
Vậy: 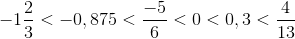
Bài 22 Sắp xếp các số hữu tỉ sau theo thứ tự lớn dần:
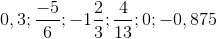
Lời giải:
Viết các phân số dưới dạng tối giản:
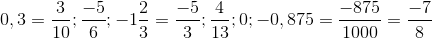
- So sánh các số hữu tỉ dương với nhau:
Ta có : 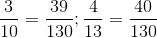
Vì 39 < 40 và 130 > 0 nên 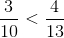
- Tương tự So sánh các số hữu tỉ âm với nhau
Vậy: 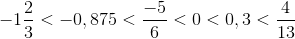

Viết các phân số dưới dạng tối giản:
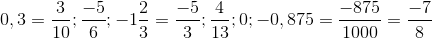
- So sánh các số hữu tỉ dương với nhau:
Ta có : 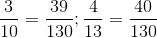
Vì 39 < 40 và 130 > 0 nên 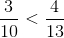
- Tương tự So sánh các số hữu tỉ âm với nhau
Vậy: 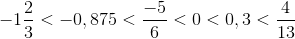

a: 0,5=1/2
-1/-3=1/3
0=0
0,25=1/4
Thứ tự tăng dần là: \(-\dfrac{1}{4}< 0< \dfrac{1}{4}< \dfrac{1}{3}< \dfrac{1}{2}\)
b: \(=\dfrac{-3}{5}-\dfrac{3}{4}+\dfrac{3}{4}-\dfrac{2}{5}=-1\)

Viết các phân số dưới dạng tối giản:
- So sánh các số hữu tỉ dương với nhau:
Ta có :
Vì 39 < 40 và 130 > 0 nên
- Tương tự So sánh các số hữu tỉ âm với nhau
Vậy:
Các số hữu tỉ được sắp sếp theo thứ tự lớn dần là:
\(-0,875< -\frac{5}{6}< -\frac{1}{3}< 0< 0,3\)
![]() ^...^
^...^ ![]() ^_^
^_^

