
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

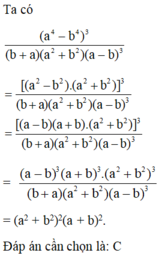

Ta có
\(M=a+\frac{2a+b}{2-b}+\frac{2a-b}{2+b}+\frac{4a}{b^2-4}\)
\(=a-\frac{2a+b}{b-2}+\frac{2a-b}{2+b}+\frac{4a}{\left(b-2\right)\left(b+2\right)}\)
\(=\frac{a\left(b-2\right)\left(2+b\right)-\left(2a+b\right)\left(2+b\right)+\left(2a-b\right)\left(b-2\right)+4a}{\left(b-2\right)\left(2+b\right)}\)
\(=\frac{ab^2-4a-4a-2ab-2b-b^2+2ab-4a-b^2+2b+4a}{\left(b-2\right)\left(2+b\right)}\)
\(=\frac{ab^2-8a-b^2}{\left(b-c\right)\left(b+2\right)}\)
Với \(b=\frac{a}{a+1}\)ta có
\(=\frac{a\cdot\frac{a^2}{a^2+2a+1}-8a-\frac{a^2}{a^2+2a+1}}{\left(\frac{a}{a+1}-2\right)\left(\frac{a}{a+1}+2\right)}\)
\(\frac{a\cdot\frac{a^2}{a^2+2a+1}-8a-\frac{a^2}{a^2+2a+1}}{\left(\frac{-a-1}{a+1}\right)\left(\frac{3a+1}{a+1}\right)}\)
\(=\frac{a\cdot\frac{a^2}{a^2+2a+1}-8a-\frac{a^2}{a^2+2a+1}}{\frac{1-3a}{a+1}}\)
\(=\frac{a\left(\frac{a^2}{a^2+2a+1}-8-\frac{a}{a^2+2a+1}\right)}{\frac{1-3a}{a+1}}\)
\(=\frac{a\left(\frac{-7a^2+15a+8}{a^2+2a+1}\right)}{\frac{1-3a}{a+1}}\)
tới đây tịt rồi ai làm tiếp đc k

a) \(a^4-5a^2+4=\)\(\left(a^4-4a^2\right)-\left(a^2-4\right)=a^2\left(a^2-4\right)-\left(a^2-4\right)=\left(a^2-1\right)\left(a^2-4\right)\)
\(=\left(a-1\right)\left(a+1\right)\left(a-2\right)\left(a+2\right)\)
\(a^4-a^2+4a-4=a^2\left(a^2-1\right)+4\left(a-1\right)=a^2\left(a-1\right)\left(a+1\right)+4\left(a-1\right)\)
\(=\left(a-1\right)\left[a^2\left(a+1\right)+4\right]=\left(a-1\right)\left(a^3+a^2+4\right)\)
\(a^3+a^2+4=\left(a^3+2a^2\right)-\left(a^2+2a\right)+\left(2a+4\right)=a^2\left(a+2\right)-a\left(a+2\right)+2\left(a+2\right)\)
\(=\left(a^2-a+2\right)\left(a+2\right)\)
\(N=\frac{\left(a-1\right)\left(a+1\right)\left(a-2\right)\left(a+2\right)}{\left(a-1\right)\left(a+2\right)\left(a^2-a+2\right)}=\frac{\left(a+1\right)\left(a-2\right)}{a^2-a+2}\)

c)\(P=\)\(\frac{\left(a-b\right)^2-c^2}{\left(a-b+c\right)^2}=\frac{\left(a-b+c\right)\left(a-b-c\right)}{\left(a-b+c\right)^2}=\frac{a-b-c}{a-b+c}\)
b)\(M\)\(=\frac{\left(a+2\right)\left(a-1\right)^2}{\left(2a-3\right)\left(a-1\right)^2}=\frac{a+2}{2a-3}\)

a, Gợi ý nà :3
a^2 + b^2 - c^2 +2ab = (a^2 + b^2 + 2ab) -c^2 = (a+b)^2 - c^2 = (a + b - c)(a + b + c)
a^2 - b^2 + c^2 + 2ac = (a + c)^2 - b^2 = (a + b + c)(a - b + c)
b. Gợi ý tiếp luôn nà :3
a^3 + b^3 + c^3 - 3abc
= (a^3 + b^3 +3a^2 x b + 3ab^2) - 3ab(a+b) -3abc + c^3
= (a+b)^3 + c^3 - 3ab(a+b+c)
= (a + b+ c)[(a+b)^2 - c(a+b) +c^2] - 3ab(a+b+c)
=(a+b+c)(a^2 + b^2 + c^2 -ac -bc + 2ab -3ab)
=(a+b+c)(a^2 + b^2 + c^2 - ab - bc -ca)
Rồi cứ thế rút gọn...
Học tốt nha bạn :3
\(\frac{a^2+2ab+b^2-c^2}{a^2+2ac+c^2-b^2}=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{\left(a+b+c\right)\left(a-b+c\right)}=\frac{a+b-c}{a-b+c}\)
\(\text{nhận xét: ta có hằng đẳng thức:}\)
\(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
đó đến đây bạn làm tiếp

c) \(\frac{a\left(a^2-ab+b^2\right)}{b\left(a+b\right)\left(a^2-ab+b^2\right)}\)
=\(\frac{a}{b\left(a+b\right)}\)

\(\frac{a^2\left(b-c\right)+b^2\left(c-a\right)+c^2\left(a-b\right)}{^{^{ }}a^4\left(b^2-c^2\right)+b^4\left(c^2-a^2\right)+c^4\left(a^2-b^2\right)}\)
=\(\frac{a^2b-a^2c+b^2c-b^2a+c^2a-c^2b}{a^4b^2-a^4c^2+b^4c^2-b^4a^2+c^4a^2-c^4b^2}\)
*Rút gọn âm và dương đối nhau ( VD: \(a^2\)và\(-a^2\)), còn lại bạn tự tìm thêm nhé :)
\(\frac{b-c+c-a+a-b}{b^2-c^2+c^2-a^2+a^2-b^2}\)
Ta lại rút gọn các cặp đối nhau ( như trên VD)
Kết quả cuối cùng là 0
Đặt biểu thức đã cho là A
Xét tử: \(a^2\left(b-c\right)+b^2\left(c-a\right)+c^2\left(a-b\right)\)
\(=a^2b-a^2c+b^2c-b^2a+c^2\left(a-b\right)\)
\(=\left(a^2b-b^2a\right)-\left(a^2c-b^2c\right)+c^2\left(a-b\right)\)
\(=ab\left(a-b\right)-c\left(a-b\right)\left(a+b\right)+c^2\left(a-b\right)\)
\(=ab\left(a-b\right)-\left(a-b\right)\left(ca+bc\right)+c^2\left(a-b\right)\)
\(=\left(a-b\right)\left(ab-ca-bc+c^2\right)\)\(=\left(a-b\right)\left[a\left(b-c\right)-c\left(b-c\right)\right]=\left(a-b\right)\left(a-c\right)\left(b-c\right)\)
Xét mẫu : làm tương tự như trên ta được
\(a^4\left(b^2-c^2\right)+b^4\left(c^2-a^2\right)+c^4\left(a^2-b^2\right)=\left(a^2-b^2\right)\left(a^2-c^2\right)\left(b^2-c^2\right)\)
\(=\left(a-b\right)\left(a+b\right)\left(a-c\right)\left(a+c\right)\left(b-c\right)\left(b+c\right)\)
\(\Rightarrow A=\frac{1}{\left(a+b\right)\left(a+c\right)\left(b+c\right)}\)
