Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(\frac{y}{x}.\left(\sqrt{\frac{x^2}{y^4}}\right)=\frac{y}{x}.\frac{x}{y^2}=\frac{1}{y}\)
b/ \(2y^2.\sqrt{\frac{x^4}{4y^2}}=2y^2.\sqrt{\frac{\left(x^2\right)^2}{\left(-2y\right)^2}}=2y^2.\frac{x^2}{-2y}=-y.x^2\)
c/ \(5xy.\sqrt{\frac{25x^2}{y^6}}=5xy.\sqrt{\frac{\left(-5x\right)^2}{\left(y^3\right)^2}}=5xy.\frac{-5x}{y^3}=\frac{-25x^2}{y^2}\)
d/\(0,2.x^3y^3.\sqrt{\frac{4^2}{\left(x^2y^4\right)^2}}=\frac{1}{5}.x^3y^3.\frac{4}{x^2y^4}=\frac{4x}{5y}\)
Trần Việt Linh sai phần b,c,d r bn
Sửa lại:
b) 2y\(^2\).\(\sqrt{\frac{x^4}{4y^2}}\) với y<0
Ta có : 2y\(^2\).\(\sqrt{\frac{x^4}{4y^2}}\)=2y\(^2\).\(\frac{x^2}{\left|y\right|}\)
Vì y>0 nên |y| = -y.Ta có : 2y\(^2\).\(\frac{x^2}{2\left|y\right|}\)= -2y\(^2\).\(\frac{x^2}{2y}\) = -2x\(^2\)y
c) 5xy.\(\sqrt{\frac{25x^2}{y^6}}\) với x<0,y>0
Ta có :5xy\(\sqrt{\frac{25x^2}{y^6}}\)=5xy.\(\frac{5\left|x\right|}{y^3}\) ( y>0)
Vì x<0 nên |x| =-x .Ta có : 5xy.\(\frac{5\left|x\right|}{y^3}\)= -5xy.\(\frac{5x}{y^3}\) =\(\frac{-25x^2}{y^2}\)
d) 0,,2x\(^3\)y\(^3\).\(\sqrt{\frac{16}{x^4y^8}}\) với x#o,y#0
Ta có: 0,2x\(^3\)y\(^3\)\(\frac{4}{x^2y^4}\)=\(\frac{0,8x}{y}\) ( vì #0,y#0)

\(A=\frac{x}{y}.\frac{x}{y^2}=\frac{x^2}{y^3}\left(\text{vì }x>0;y< 0\text{ nên: }\frac{x}{y^2}>0\right)\)
\(A=\frac{x}{y}\cdot\sqrt{\frac{x^2}{y^4}}=\frac{x}{y}\cdot\frac{\sqrt{x^2}}{\sqrt{y^4}}=\frac{x}{y}\cdot\frac{\left|x\right|}{\left|y^2\right|}=\frac{x}{y}\cdot\frac{x}{y^2}=\frac{x^2}{y^3}\)( x > 0 ; y < 0 )

(Vì x > 0 nên |x| = x; y2 > 0 với mọi y ≠ 0)
(Vì x2 ≥ 0 với mọi x; và vì y < 0 nên |2y| = – 2y)
(Vì x < 0 nên |5x| = – 5x; y > 0 nên |y3| = y3)
(Vì x2y4 = (xy2)2 > 0 với mọi x ≠ 0, y ≠ 0)

a. Ta có:\(\frac{x}{y}\sqrt{\frac{y^2}{x^4}=}\) \(\frac{x}{y}.\frac{\left|y\right|}{x^2}=\frac{x.y}{x^2y}\)\(=\frac{1}{x}\)(Vì \(x\ne0;y>0\))
b \(3x^2\sqrt{\frac{8}{x^2}}=3x^2\frac{2\sqrt{2}}{\left|x\right|}=\frac{6x^2\sqrt{2}}{-x}=-6x\sqrt{2}\)( Vì \(x< 0\))

a) \(\frac{\sqrt{2x^3}}{\sqrt{8x}}=\sqrt{\frac{2x^3}{8x}}=\frac{1}{2}x\)
b) \(\left(3-\sqrt{5}\right)\left(x+\sqrt{5}\right)=3^2-\left(\sqrt{5}\right)^2=9-5=4\)
c) \(\sqrt{\frac{3x^2y^4}{27}}=0\)
\(y\ne0\)
Thì \(\sqrt{\frac{3x^2y^4}{27}}=\frac{1}{3}xy^2\)
e) \(\frac{y}{x^2}\sqrt{\frac{36x^4}{y^2}}=\frac{y}{x^2}.\frac{6x^2}{\left|y\right|}=\frac{6y}{\left|y\right|}\)
Vì y < 0 nên \(\left|y\right|=-y\)
Vậy \(\frac{6y}{\left|y\right|}=\frac{6y}{-y}=-6\)
f) \(\frac{\sqrt{99999999}}{\sqrt{11111111}}=\sqrt{\frac{99999999}{11111111}}=\sqrt{9}=3\)

\(a,\frac{\sqrt{108x^3}}{\sqrt{12x}}=\frac{\sqrt{36.3.x^3}}{\sqrt{3.4.x}}=\frac{6\sqrt{3}.\sqrt{x}^3}{2\sqrt{3}.\sqrt{x}}=3\sqrt{x}^2=3x\)
\(b,\frac{\sqrt{13x^4y^6}}{\sqrt{208x^6y^6}}=\frac{\sqrt{13}.\sqrt{x^4}.\sqrt{y^6}}{\sqrt{16.13}.\sqrt{x^6}.\sqrt{y^6}}=\frac{\sqrt{13}.x^2y^3}{4\sqrt{13}x^3y^3}=\frac{1}{4x}\)
\(c,\frac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}-\left(\sqrt{x}+\sqrt{y}\right)^2\)
\(=\frac{\sqrt{x}^3+\sqrt{y}^3}{\sqrt{x}+\sqrt{y}}-\left(x+2\sqrt{xy}+y\right)\)
\(=\frac{\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)}{\sqrt{x}+\sqrt{y}}-x-2\sqrt{xy}-y\)
\(=x-\sqrt{xy}+y-x-2\sqrt{xy}-y=-3\sqrt{xy}\)
\(d,\sqrt{\frac{x-2\sqrt{x}+1}{x+2\sqrt{x}+1}}=\frac{\sqrt{\left(\sqrt{x}-1\right)^2}}{\sqrt{\left(\sqrt{x}+1\right)^2}}=\frac{\sqrt{x}-1}{\sqrt{x}+1}\)
Đk chỗ này là \(\sqrt{x}-1\ge0\Rightarrow\sqrt{x}\ge\sqrt{1}\Rightarrow x\ge1\)nhé
\(e,\frac{x-1}{\sqrt{y}-1}.\sqrt{\frac{\left(y-2\sqrt{y}+1\right)^2}{\left(x-1\right)^4}}=\frac{x-1}{\sqrt{y}-1}.\frac{y-2\sqrt{y}+1}{\left(x-1\right)^2}\)
\(=\frac{\left(x-1\right)\left(\sqrt{y}-1\right)^2}{\left(\sqrt{y}-1\right)\left(x-1\right)^2}=\frac{\sqrt{y}-1}{x-1}\)

\(A=\frac{y}{x}\cdot\sqrt{\frac{x^2}{y^4}}=\frac{y}{x}\cdot\frac{\sqrt{x^2}}{\sqrt{y^4}}=\frac{y}{x}\cdot\frac{\left|x\right|}{\left|y^2\right|}=\frac{y}{x}\cdot\frac{x}{y^2}=\frac{1}{y}\)( x > 0 ; y > 0 )

a) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\y\ge0\\x\ne y\end{matrix}\right.\)
Gọi biểu thức trên là A , ta có:
\(A=\frac{2\left(\sqrt{x}-\sqrt{y}\right)}{\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)}+\frac{\sqrt{x}+\sqrt{y}}{\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)}-\frac{3\sqrt{x}}{\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)}\\ =\frac{2\sqrt{x}-2\sqrt{y}+\sqrt{x}+\sqrt{y}-3\sqrt{x}}{\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)}\\ =\frac{-\sqrt{y}}{x-y}\left(=\frac{\sqrt{y}}{y-x}\right)\)
b) Với x=4 ; y=9 ta có:
\(A=\frac{\sqrt{9}}{9-4}=\frac{3}{5}\)
c) Ta có: với x>y>0 thì A<=>\(\left\{{}\begin{matrix}\sqrt{y}>0\\x>y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{y}>0\\y-x< 0\end{matrix}\right.\Leftrightarrow A< 0\)
Vậy A<0 với mọi x>y>0
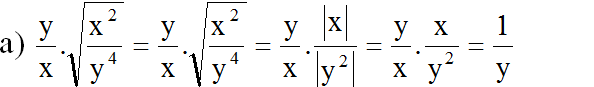
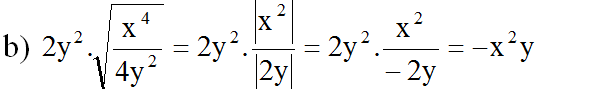
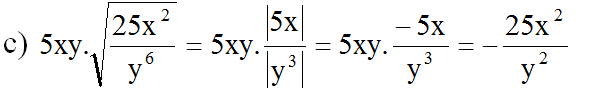
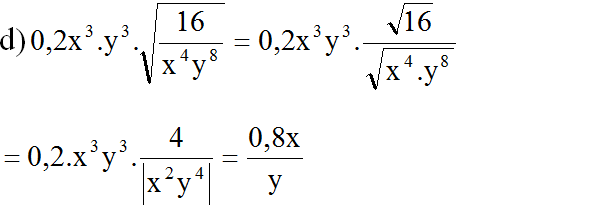
(Vì x > 0 nên |x| = x; y 2 > 0 với mọi y ≠ 0)
(Vì x 2 ≥ 0 với mọi x; và vì y < 0 nên |2y| = – 2y)
(Vì x 2 y 4 = ( x y 2 ) 2 > 0 với mọi x ≠ 0, y ≠ 0)
(Vì x < 0 nên |5x| = – 5x; y > 0 nên | y 3 | = y 3 )