
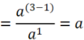
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

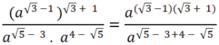
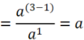

a) =
=
b) =
=
=
. ( Với điều kiện b # 1)
c) \(\dfrac{a^{\dfrac{1}{3}}b^{-\dfrac{1}{3}-}a^{-\dfrac{1}{3}}b^{\dfrac{1}{3}}}{\sqrt[3]{a^2}-\sqrt[3]{b^2}}\)= =
=
( với điều kiện a#b).
d) \(\dfrac{a^{\dfrac{1}{3}}\sqrt{b}+b^{\dfrac{1}{3}}\sqrt{a}}{\sqrt[6]{a}+\sqrt[6]{b}}\) = =
=
=

Với mọi \(k\ge2\) thì \(\frac{2k+\sqrt{k^2-1}}{\sqrt{k-1}+\sqrt{k+1}}=\frac{\left[\left(\sqrt{k-1}\right)^2+\left(\sqrt{k+1}\right)^2+\sqrt{\left(k-1\right)\left(k+1\right)}\right]\left(\sqrt{k+1}-\sqrt{k-1}\right)}{\left(\sqrt{k-1}+\sqrt{k+1}\right)\left(\sqrt{k+1}-\sqrt{k-1}\right)}\)
\(=\frac{\sqrt{\left(k+1\right)^3}-\sqrt{\left(k-1\right)^3}}{2}\)
Suy ra tổng đã cho có thể viết là :
\(A=\frac{1}{2}\left[\sqrt{3^3}-\sqrt{1^3}+\sqrt{4^3}-\sqrt{2^3}+\sqrt{5^3}-\sqrt{3^3}+\sqrt{6^3}-\sqrt{4^3}+...+\sqrt{101^3}-\sqrt{99^3}\right]\)
\(=\frac{1}{2}\left[-1-\sqrt{2^3}+\sqrt{101^3}+\sqrt{100^3}\right]\)
\(=\frac{999+\sqrt{101^3}-\sqrt{8}}{2}\)

a) \(A=\left[\left(\frac{1}{5}\right)^2\right]^{\frac{-3}{2}}-\left[2^{-3}\right]^{\frac{-2}{3}}=5^3-2^2=121\)
b) \(B=6^2+\left[\left(\frac{1}{5}\right)^{\frac{3}{4}}\right]^{-4}=6^2+5^3=161\)
c) \(C=\frac{a^{\sqrt{5}+3}.a^{\sqrt{5}\left(\sqrt{5}-1\right)}}{\left(a^{2\sqrt{2}-1}\right)^{2\sqrt{2}+1}}=\frac{a^{\sqrt{5}+3}.a^{5-\sqrt{5}}}{a^{\left(2\sqrt{2}\right)^2-1^2}}\)
\(=\frac{a^{\sqrt{5}+3+5-\sqrt{5}}}{a^{8-1}}=\frac{a^8}{a^7}=a\)
d) \(D=\left(a^{\frac{1}{2}}-b^{\frac{1}{2}}\right)^2:\left(b-2b\sqrt{\frac{b}{a}}+\frac{b^2}{a}\right)\)
\(=\left(\sqrt{a}-\sqrt{b}\right)^2:b\left[1-2\sqrt{\frac{b}{a}}+\left(\sqrt{\frac{b}{a}}\right)^2\right]\)
\(=\left(\sqrt{a}-\sqrt{b}\right)^2:b\left(1-\sqrt{b}a\right)^2\)

Lời giải:
Ta có \(A=\frac{a^{\frac{1}{3}}-a^{\frac{7}{3}}}{a^{\frac{1}{3}}-a^{\frac{4}{3}}}-\frac{a^{\frac{1}{3}}-a^{\frac{5}{3}}}{a^{\frac{2}{3}}+a^{\frac{1}{3}}}\)
\(=\frac{\sqrt[3]{a}-\sqrt[3]{a^7}}{\sqrt[3]{a}-\sqrt[3]{a^4}}-\frac{\sqrt[3]{a}-\sqrt[3]{a^5}}{\sqrt[3]{a^2}+\sqrt[3]{a}}\)
\(=\frac{\sqrt[3]{a}(1-a^2)}{\sqrt[3]{a}(1-a)}-\frac{\sqrt[3]{a}(1-\sqrt[3]{a^4})}{\sqrt[3]{a}(1+\sqrt[3]{a})}=\frac{1-a^2}{1-a}-\frac{1-\sqrt[3]{a^4}}{1+\sqrt[3]{a}}\)
\(=1+a-\frac{1-\sqrt[3]{a^4}}{1+\sqrt[3]{a}}\)
Đặt \(\sqrt[3]{a}=t\Rightarrow A=1+t^3-\frac{1-t^4}{1+t}=1+t^3-\frac{(1-t^2)(1+t^2)}{1+t}\)
\(=1+t^3-\frac{(1-t)(1+t)(1+t^2)}{1+t}=1+t^3-(1-t)(1+t^2)\)
\(=2t^3-t^2+t\)

\(I=\frac{a^{\frac{4}{3}}-8a^{\frac{2}{3}}b}{a^{\frac{2}{3}}+2\sqrt[3]{ab}+4b^{\frac{2}{3}}}\left(1-2\sqrt[3]{\frac{b}{a}}\right)^{-1}-a^{\frac{2}{3}}=\frac{a^{\frac{1}{3}}\left(a-8b\right)}{a^{\frac{2}{3}}+2a^{\frac{1}{3}}.b^{\frac{1}{3}}+4b^{\frac{2}{3}}}\left(\frac{\sqrt[3]{a}-2\sqrt[3]{b}}{\sqrt[3]{a}}\right)^{-1}-a^{\frac{2}{3}}\)
\(=\frac{\sqrt[3]{a}\left[\left(\sqrt[3]{a}\right)^3-\left(2\sqrt[3]{b}\right)^3\right]}{a^{\frac{2}{3}}+2\sqrt[3]{ab}+4b^{\frac{2}{3}}}.\frac{\sqrt[3]{a}}{\sqrt[3]{a}-2\sqrt[3]{b}}-a^{\frac{2}{3}}\)
\(=\frac{\left(\sqrt[3]{a}\right)^2\left(\sqrt[3]{a}-2\sqrt[3]{b}\right)\left[\left(\sqrt[3]{a}\right)^2+2\sqrt[3]{ab}+\left(2\sqrt[3]{b}\right)^2\right]}{\left(\sqrt[3]{a}-a\sqrt[3]{b}\right)\left[\left(\sqrt[3]{a}\right)^2+2\sqrt[3]{ab}+\left(2\sqrt[3]{b}\right)^2\right]}-a^{\frac{2}{3}}=a^{\frac{2}{3}}-a^{\frac{2}{3}}=0\)

Theo công thức biến đổi có số ta có : \(\log_{a^n}x=\frac{\log_ax}{\log_aa^n}=\frac{1}{n}\log_ax\)
Từ đó ta có :
\(A=\frac{1}{\log_ax}+\frac{1}{\log_{a^2}x}+\frac{1}{\log_{a^3}x}+...+\frac{1}{\log_{a^n}x}\)
\(=\frac{1}{\log_ax}+\frac{2}{\log_ax}+\frac{4}{\log_ax}+...+\frac{n}{\log_ax}\)
\(=\frac{1+2+3+...+n}{\log_ax}=\frac{n\left(n+1\right)}{\log_ax}\)
Vậy \(A=\frac{1}{\log_ax}+\frac{1}{\log_{a^2}x}+\frac{1}{\log_{a^3}x}+...+\frac{1}{\log_{a^n}x}=\frac{n\left(n+1\right)}{\log_ax}\)
