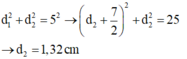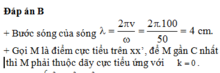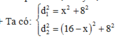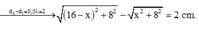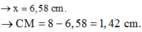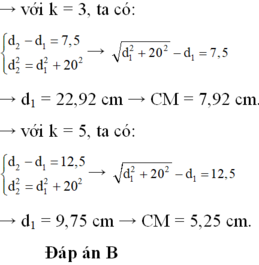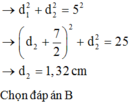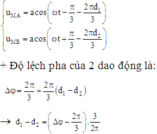Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

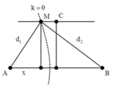
A B P d M d x d1 d2
\(d_1 - d_2 = \left( {\phi _m - \phi } \right)\dfrac{\lambda }{{2\pi }} = \left( {2k + 1} \right)\dfrac{{0.5\pi }}{{2\pi }} = \dfrac{k}{2} + 0.25 \)
Điểm M gần hất \(\Rightarrow k = 0 \Rightarrow d_1 - d_2 = 0.25 \)
\(\Rightarrow \sqrt {(\dfrac{d}{2} + x)^2 + 100^2 } - \sqrt {(\dfrac{d}{2} - x)^2 + 100^2 } = 0.25 \)
\(\Rightarrow \sqrt {(\dfrac{1}{2} + x)^2 + 100^2 } - \sqrt {(\dfrac{1}{2} - x)^2 + 100^2 } = 0.25 \)
\(\Rightarrow x = 25.82 m\)

Đáp án D
+ Số dãy cực đại trên đoạn
![]()
+ Để CM là lớn nhất thì M thuộc hypebol ứng với k=2
Ta có d 1 - d 2 = 8 cm
+ Với:
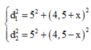
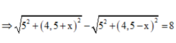
![]()
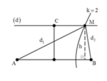

chọn đáp án A
Hai nguồn cùng pha nên trung điểm hai nguồn là một cực đại, M cách O gần nhấ là 1,5 dao động với biên độ cực đại nên
λ
=
3
c
m
Hai nguồn dao động cùng pha nên số điểm dao động với biên độ cực đại trên đường nối hai nguồn ứng với giá trị k thuộc
-
A
B
λ
;
A
B
λ
⇔
-
5
;
5
→có 9 giá trị
Do đường kính của đường tròng tâm O là 20 →hai nguồn nằm trong đường tròn nên số điểm dao động với biên độ cực đại trên đường tròn là 18 điểm

- Phương trình dao động của M đối với 2 nguồn là:
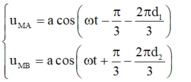
- Độ lệch pha của 2 dao động là:
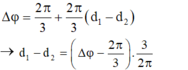
- M dao động với biên độ cực tiểu nên ta có:
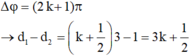
- Số điểm dao động với biên độ cực tiểu trên AB là:
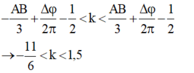
- Mà M cách B đoạn nhỏ nhất:
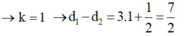
- Lại có: