

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án: D
Nhiệt độ để chiều dài của chúng bằng nhau:
l0nh(1 + anht) = l0s(1 + ast)
(ban đầu t0 = 0 oC → ∆t = t)
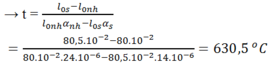
Nhiệt độ để thể tích của chúng bằng nhau:
S0l0nh(1 + 3anht’) = S0l0s(1 + 3ast’)
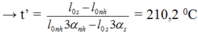

Đáp án: D
Nhiệt độ để chiều dài của chúng bằng nhau:
l0nh(1 + anht) = l0s(1 + ast) (ban đầu t0 = 0 oC → ∆t = t)
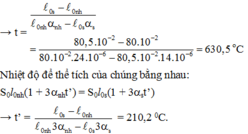

a/ Chiều dài của thanh: \(l=l_0(1+\alpha.\Delta t)\)
Thanh nhôm: \(l=50.[1+24.10^{-6}.(170-20)]=50,18cm\)
Thanh thép: \(l=50,12.[1+12.10^{-6}.(170-20)]=50,21cm\)
b/ Giả sử ở nhiệt độ t, hai thanh có cùng chiều dài
\(\Rightarrow 50.[1+24.10^{-6}.(t-20)]=50,12.[1+12.10^{-6}.(t-20)]\)
Bạn giải phương trình trên rồi tìm t nhé ![]()

Tóm tắt: \(l_{01}=100mm;l_{02}=101mm\)
\(\alpha_1=2,4\cdot10^{-5}K^{-1};\alpha_2=1,2\cdot10^{-5}K^{-1}\)
Lời giải:
a)Chiều dài thanh nhôm ở \(t^oC\) là:
\(l_1=l_{01}\cdot\left[1+\alpha_1\left(t-t_0\right)\right]=100\cdot\left[1+2,4\cdot10^{-5}\cdot\left(t-20\right)\right]\)
Chiều dài thanh sắt \(t^oC\) là:
\(l_2=l_{02}\cdot\left[1+\alpha_2\left(t-t_0\right)\right]=101\cdot\left[1+1,2\cdot10^{-5}\cdot\left(t-20\right)\right]\)
Để hai thanh có chiều dài bằng nhau.\(\Rightarrow l_1=l_2\)
\(100\cdot\left[1+2,4\cdot10^{-5}\cdot\left(t-20\right)\right]=101\cdot\left[1+1,2\cdot10^{-5}\cdot\left(t-20\right)\right]\)
\(\Rightarrow t=861,75^oC\)
b)Hệ số nở khối: \(\beta=3\alpha\)
Thể tích thanh nhôm ở \(t^oC\) là:
\(V_1=V_{01}\cdot\left[1+\beta_1\left(t-t_0\right)\right]=100s\cdot\left[1+3\cdot2,4\cdot10^{-5}\left(t-20\right)\right]\)
Thể tích thanh sắt ở \(t^oC\) là:
\(V_2=V_{02}\cdot\left[1+\beta_2\left(t-t_0\right)\right]=101s\cdot\left[1+3\cdot1,2\cdot10^{-5}\cdot\left(t-20\right)\right]\)
Để hai thanh có thể tích bằng nhau: \(V_1=V_2\)
\(\Rightarrow100s\cdot\left[1+3\cdot2,4\cdot10^{-5}\cdot\left(t-20\right)\right]=101s\cdot\left[1+3\cdot1,2\cdot10^{-5}\cdot\left(t-20\right)\right]\)
\(\Rightarrow t=21,4^oC\)

Để thanh ray không bị cong khi nhiệt độ tăng thì độ tăng chiều dài của thanh phải bằng khoảng cách giữa hai đầu thanh ray.
∆l = l2 - l1 = l1α(t2 – t1)
=> t2 = tmax = △lαl1△lαl1+ t1= 4,5.10−312.10−6..12,54,5.10−312.10−6..12,5 + 15
=> tmax = 45o.

* Cách 1 :
Khoảng cách giữa 2 thanh ray liên tiếp nhau chính là độ nở dài của mỗi thanh .
Ta có : △l = l0a . △t
→ Độ biến dạng thiên nhiệt độ △t :
△t = \(\frac{\triangle l}{l_0.a}=\frac{4,5.10^{-3}}{12,5.12.10^{-8}}=0,03.10^3=30^oC\)
Nhiệt độ môi trường lớn nhất để thanh ray không bị cong :
tmax = △t + t = 15oC + 30oC = 45oC
Đáp số 450C
* Cách 2 :
Để thanh ray không bị cong khi nhiệt độ tăng thì độ tăng chiều dài của thanh phải bằng khoảng cách giữa hai đầu thanh ray.
∆l = l2 - l1 = l1α(t2 – t1)
=> t2 = tmax = + t1=
+ 15
=> tmax = 45o

Để thanh ray không bị cong khi nhiệt độ tăng thì độ tăng chiều dài của thanh phải bằng khoảng cách giữa hai đầu thanh ray.
∆l = l2 - l1 = l1α(t2 – t1)
=> t2 = tmax = + t1=
+ 15
=> tmax = 45o.
Khoảng cách giữa 2 thanh ray liên tiếp nhau chính là độ nở dài của mỗi thanh .
Ta có : \(\triangle\)l = l0a . \(\triangle\)t
→ Độ biến dạng thiên nhiệt độ \(\triangle\)t :
\(\triangle t=\frac{\triangle l}{l_0.a}=\frac{4,5.10^{-3}}{12,5.12.10^{-6}}=0,03.10^3=30\) độ C
Nhiệt độ môi trường lớn nhất để thanh ray không bị cong :
tmax = \(\triangle\)t + t = 15 độ C + 30 độ C = 45 độ C
Đáp số 45 độ C

Gọi \(t_2\) là nhiệt độ để hai sợi chênh lệch nhau 0,3cm.
Độ dài sợi đồng ở \(t_2\left(^oC\right)\) là:
\(l_1=l_{01}\cdot\left(1+\alpha_1\cdot\Delta t\right)=4\cdot\left(1+17,2\cdot10^{-6}\cdot\left(t_2-10\right)\right)\)
Độ dài sợi dây sắt ở \(t_2\left(^oC\right)\) là:
\(l_2=l_{02}\left(1+\alpha_2\cdot\Delta t\right)=4\cdot\left(1+11,4\cdot10^{-6}\cdot\left(t_2-10\right)\right)\)
Để chúng lệch nhau \(0,3cm=0,003m\).
\(\Rightarrow\Delta l=l_1-l_2\)
\(\Rightarrow\Delta l=4\cdot\left(1+17,2\cdot10^{-6}\cdot\left(t_2-10\right)\right)-4\cdot\left(1+11,4\cdot10^{-6}\cdot\left(t_2-10\right)\right)=0,003\)
\(\Rightarrow t_2=139,31^oC\)