Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:\(P=F_{kéo}=10m=10.50=500N\)
Vì đây là hệ hai ròng rọc. một cố định và một là ròng rọc động, vật đặt ở ròng rọc động thì khi kéo sợi dây được 50 cm = 0,5 m thì vật được nâng lên 0,25m (do chia đều dây hai bên ròng rọc động)
=> Công của lực kéo là: \(A=F.s=500.0,25=125\left(J\right)\)
b)
Xét đoạn dây gắn trực tiếp với xà: Do hai bên dây của ròng rọc động chịu lực như nhau nên ta có: lực kéo xuống ở vị trí này là \(F_1=250N\)
Xét đoạn dây vòng qua ròng rọc cố định: Do ròng rọc cố định chỉ có tác dụng đổi phương lực kéo nên ở vị trí này xà cũng chịu một lực \(F_2=250N\)
Vậy xà sẽ chịu một lực \(F=F_1+F_2=250+250=500N\). Đó chính là trọng lượng của vật

t = 2 phút = 120s
m = 100kg
h = 12m
s = 40m
Ta có Fk = Px
Fk = m.g.sina = m.g.\(\frac{h}{s}\)= 300N
A = Fk.s.cos0 = 12000J
Ahp = Fms.s.cos180 = -1400J
H = \(\frac{A}{Atp}\) .100% = 89.55%

Vì s = 1,6m; h = 20cm = 0,2m nên đường đi s của lực kéo F gấp 8 lần đường đi của vật. Vậy ta được lợi 8 lần về lực.
⇒ lực kéo dây là: 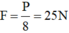
Công sinh ra là: A = F.s = 25.1,6 = 40J

\(P=10m=10\cdot400=4000N\)
Một palant được cấu tạo bởi 2 ròng rọc động và 2 ròng rọc cố định\(\Rightarrow\) thiệt 2 lần về lực và lợi hai lần về đường đi.
a)\(F=\dfrac{1}{2}P=2000N\)
b)Phải kéo dây một đoạn:
\(A=F\cdot s=P\cdot h\)
\(\Rightarrow s=\dfrac{P\cdot h}{F}=\dfrac{4000\cdot5}{2000}=10m\)

a. Công của trọng lực cũng bằng công của lực kéo :
A=F.s=P.h=10.m.h=10.60.4=2400(J)
b. - Do dùng dòng dọc động nên cho ta lợi 2 lần về lực và thiệt 2 lần về đường đi nên chiều dài dây là: s=2.h=2.4=8(m)
Công toàn phần là: Atp=F.s=320.8=2560(J)
Hiệu suất của ròng rọc là: H=A/Atp.100%=93,75%

Đáp án B
- Trọng lượng của vật là: 40.10 = 400 (N)
S = 8.h.
- Như vậy dùng ròng rọc động bị thiệt 8 lần về đường đi, nên sẽ được lợi 8 lần về lực
- Lực kéo cần thiết là:
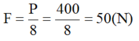
Đáp án: D
- Trọng lượng của kiện hàng là:
P = 10.m = 10.200 = 2000 (N)
- Dùng pa lăng cho ta lợi về lực 4 lần, nên sẽ bị thiệt 4 lần về đường đi. Do đó phải kéo dây đi:
4.5 = 20 (m)