Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
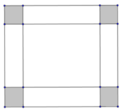
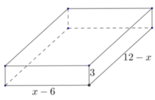
Hình hộp có đáy là hình vuông cạnh: 12 - 2x
Chiều cao của hình hộp là: x
Thể tích hình hộp là y = x ( 12 - 2 x ) 2
Bài toán đưa về tìm x ∈ (0; 6) để hàm số y = f ( x ) = x ( 12 - 2 x ) 2 có giá trị lớn nhất.
y ' = 1 ( 12 - 2 x ) 2 + x . 2 . ( 12 - 2 x ) . ( - 2 )
12 x 2 - 96 x + 144 ;
y' xác định ∀ x ∈ (0; 6)
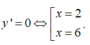
Bảng biến thiên
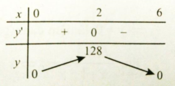
Hàm số đạt giá trị lớn nhất tại x=2

A E M B C H N S
Xét tam giác ABC có : \(BC=AB.\tan60^0=2a\sqrt{3}\Rightarrow S_{\Delta ABC}=2a^2\sqrt{3}\)
\(V_{S.ABCD}=\frac{1}{3}SA.S_{\Delta ABC}=\frac{1}{3}a\sqrt{3}.2a^2\sqrt{3}=2a^3\)
- Gọi N là trung điểm cạnh SA. Do SB//(CMN) nên d(SB. CM)=d(SB,(CMN))
=d(B,(CMN))
=d(A,(CMN))
- Kẻ \(AE\perp MC,E\in MC\) và kẻ \(AH\perp NE,H\in NE\), ta chứng minh được \(AH\perp\left(CMN\right)\Rightarrow d\left(A,\left(CMN\right)\right)=AH\)
Tính \(AE=\frac{2S_{\Delta AMC}}{MC}\) trong đó :
\(S_{\Delta AMC}=\frac{1}{2}AM.AC.\sin\widehat{CAM}=\frac{1}{2}a.4a\frac{\sqrt{3}}{2}=a^2\sqrt{3};MC=a\sqrt{13}\)
\(\Rightarrow AE=\frac{2a\sqrt{3}}{\sqrt{13}}\)
Tính được \(AH=\frac{2a\sqrt{3}}{\sqrt{29}}\Rightarrow d\left(A,\left(CMN\right)\right)=\frac{2a\sqrt{3}}{\sqrt{29}}\Rightarrow d\left(SB,CM\right)=\frac{2a\sqrt{3}}{\sqrt{29}}\)

?o?n th?ng a: ?o?n th?ng [A, D] ?o?n th?ng b: ?o?n th?ng [A, B] ?o?n th?ng e: ?o?n th?ng [B, C] ?o?n th?ng f: ?o?n th?ng [C, D] ?o?n th?ng g: ?o?n th?ng [A, C] ?o?n th?ng i: ?o?n th?ng [S, H] ?o?n th?ng j: ?o?n th?ng [S, A] ?o?n th?ng k: ?o?n th?ng [S, B] ?o?n th?ng l: ?o?n th?ng [S, C] ?o?n th?ng m: ?o?n th?ng [S, D] ?o?n th?ng n: ?o?n th?ng [M, C] ?o?n th?ng p: ?o?n th?ng [M, B] ?o?n th?ng p: ?o?n th?ng [M, B] A = (-1.48, 1.8) A = (-1.48, 1.8) A = (-1.48, 1.8) D = (2.3, 1.8) D = (2.3, 1.8) D = (2.3, 1.8) B = (-3.12, -0.08) B = (-3.12, -0.08) B = (-3.12, -0.08) ?i?m C: Giao ?i?m c?a c, d ?i?m C: Giao ?i?m c?a c, d ?i?m C: Giao ?i?m c?a c, d ?i?m H: (3A + C) / 4 ?i?m H: (3A + C) / 4 ?i?m H: (3A + C) / 4 ?i?m S: ?i?m tr�n h ?i?m S: ?i?m tr�n h ?i?m S: ?i?m tr�n h ?i?m M: (S + A) / 2 ?i?m M: (S + A) / 2 ?i?m M: (S + A) / 2
Do CM là trung tuyến của SAC nên M là trung điểm SA.
\(\dfrac{V_{SMBC}}{V_{SABC}}=\dfrac{SM}{SA}=\dfrac{1}{2}\)
Ta có \(AC=\sqrt{AB^2+AC^2}=a\sqrt{2}\) nên \(AH=\dfrac{1}{4}AC=\dfrac{a\sqrt{2}}{4}\)
Suy ra \(SH=\sqrt{SA^2-AH^2}=\sqrt{a^2-\dfrac{2a^2}{16}}=\dfrac{a\sqrt{14}}{4}\)
Do đó \(V_{SABC}=\dfrac{1}{3}SH.S_{ABC}=\dfrac{1}{3}.\dfrac{a\sqrt{14}}{4}.\dfrac{a^2}{2}=\dfrac{a^3\sqrt{14}}{24}\)
Vậy \(V_{SMBC}=\dfrac{1}{2}V_{SABC}=\dfrac{a^3\sqrt{14}}{48}\)
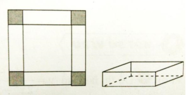

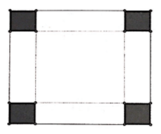



15 cm
Bàn giúp mình giải rồi chụp giúp mình nha