Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

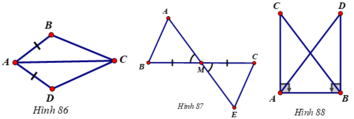
Giải: a) Bổ sung thêm \(\widehat{BAC}\)=\(\widehat{DAC}\).
b) Bổ sung thêm MA=ME.
c) Bổ sung thêm AC=BD.

a) thêm điều kiện: BÁC = DAC
b) thêm điều kiện MA=ME
c) Thêm điều kiện AC=BD
Xét tam giác ABC và tam giác ADC , có :
AB=AD
góc A1 = góc A2
AC cạnh chung
=> tam giác ABC = tam giác ADC (c.g.c)
mình chỉ làm được thế thôi , còn mấy hình kia bạn tự làm nhé
nó y hệt luôn

Tham Khảo:
https://vietjack.com/giai-toan-lop-7/bai-27-trang-119-sgk-toan-7-tap-1.jsp

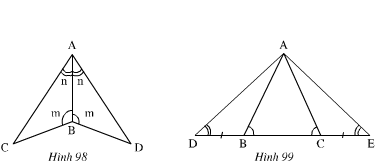
nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)

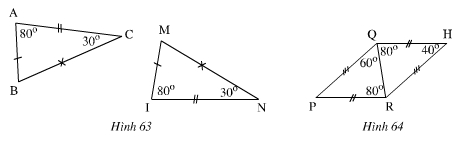
Hình 63
Ta có:
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
Hình 64 :
ΔPQR có:
Và QH = RP, HR = PQ, QR ( cạnh chung )
Nên ΔHQR = ΔPRQ

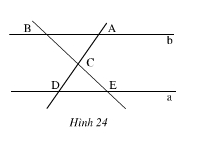
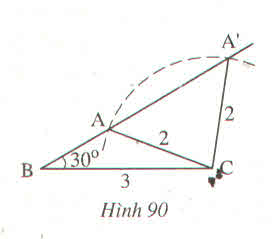
Góc ABC không phải là góc xen giữa BC và CA, Góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C' được.
Góc ABC không phải là góc xen giữa BC và CA, Góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C' được.
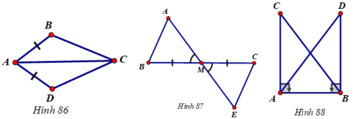
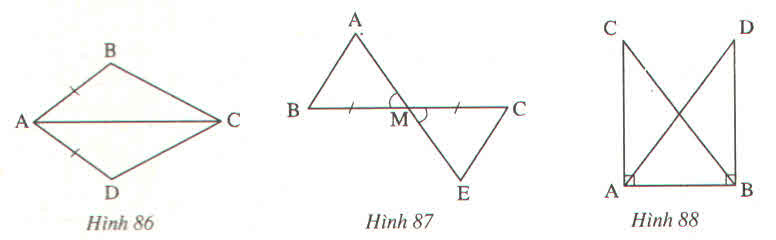
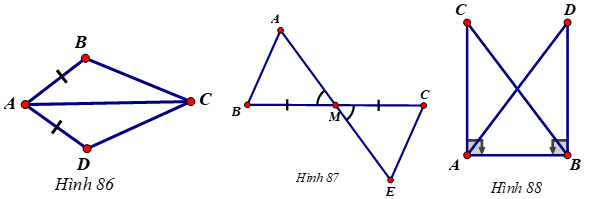
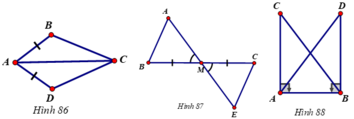





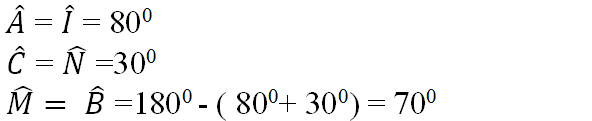
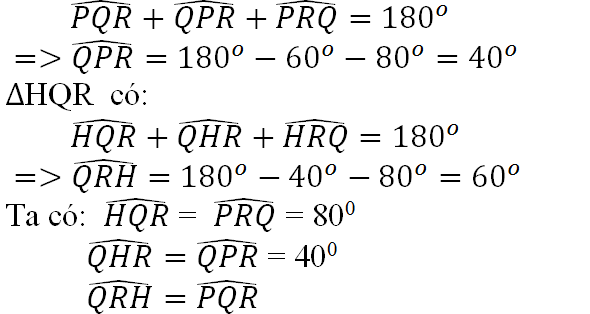
Bổ sung thêm góc BAC = góc DAC.