Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vật đã đi được 4s
\(v=9-2t\Rightarrow\left\{{}\begin{matrix}v_0=9\\a=-2\end{matrix}\right.\)
\(S=v_0t+\dfrac{1}{2}at^2=20m\)

1)
v0=0
Sgiây thứ 3 = 5m \(\Leftrightarrow S_{giâythứ3}=v_0t+\frac{1}{2}at^2-v_0\left(t-1\right)-\frac{1}{2}a\left(t-1\right)^2=v_0+a\left(t-\frac{1}{2}\right)=0+a\left(3-\frac{1}{2}\right)=\frac{5}{2}a\)
=> \(\frac{5}{2}a=5\)
=> a =2\(m/s^2\)
Quãng đường xe đi được sau 10s là:
t =10s => \(s=v_0t+\frac{1}{2}at^2=\frac{1}{2}.2.10^2=100\left(m\right)\)

Đáp án C
Từ phương trình vận tốc suy ra :
Chú ý: Có thể tính bằng công thức vtb như sau
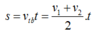
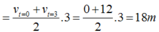

a) a=15/10=3/2
b)s=1/2x3/2x100=75m
c)s=75-1/2x3/2x81=14,25m

\(a,x=2t+t^2\left(m,s\right)\Rightarrow\left\{{}\begin{matrix}vo=2\left(m/s\right)\\xo=0\\a=2m/s^2\end{matrix}\right.\)\(\Rightarrow v=vo+at1=2+2.2=6\left(m/s\right)\)
\(b,\Rightarrow S=vo\left(t1-t2\right)+\dfrac{1}{2}a\left(t1-t2\right)^2=15m\)
\(c,Ox\equiv AB,O\equiv A,\) \(chiều\left(+\right)\) \(A->B\)
\(\Rightarrow\left\{{}\begin{matrix}xA=x=2t+t^2\\xB=90-vo't+\dfrac{1}{2}at^2=90-10t+\dfrac{1}{2}at^2=90-10t+\dfrac{1}{2}t^2\end{matrix}\right.\)\(\left(m,s\right)\)
\(\Rightarrow xA=xB\Rightarrow t=6s\Rightarrow vị\) \(trí\) \(gặp\) \(nhau\) \(cách\) \(A:xA=2.6+6^2=48m\)
Đáp án A