Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi độ dài cạnh đáy là x (cm) (x > 0)
Chiều cao của thửa ruộng có độ dài là: 360/x (cm)
Vì nếu tăng cạnh đáy lên 4m và chiều cao tương ứng giảm 1m đi thì diện tích không đổi nên ta có phương trình:
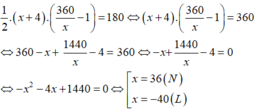
Vậy chiều dài cạnh đáy của thửa ruộng có độ dài là: 36 cm

Đáp án C
Gọi độ dài cạnh đáy là x (cm) (x > 0)
Chiều cao của thửa ruộng có độ dài là: 360/x (cm)
Vì nếu tăng cạnh đáy lên 4m và chiều cao tương ứng giảm 1m đi thì diện tích không đổi nên ta có phương trình:
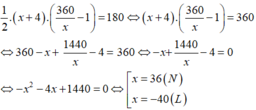
Vậy chiều dài cạnh đáy của thửa ruộng có độ dài là: 36 cm

Gọi cạnh đáy của thửa ruộng là x (x > 0)
Suy ra chiều cao của thửa ruộng là 2.180 x = 360 x (m)
Vì khi tăng cạnh đáy thêm 4m và giảm chiều cao tương ứng đi 1m thì diện tích thửa ruộng không đổi nên ta có phương trình:
1 2 . 360 x − 1 x + 4 = 180 ⇔ ( 360 – x ) ( x + 4 ) = 360 x ⇔ x 2 + 4 x – 1440 = 0
⇔ x 2 – 36 x + 40 x – 1440 = 0 ⇔ x ( x – 36 ) + 40 ( x – 36 ) = 0
⇔ ( x – 36 ) ( x + 40 ) = 0 ⇔ ⇔ x = 36 ( t m d k ) x = − 40 ( k t m d k )
Vậy cạnh đáy của thửa ruộng là 36 m
Đáp án:A

Bài làm :
Gọi chiều dài một cạnh cần tính là a (m) ; chiều cao tương ứng là h (m) . Điều kiện : a,h > 0
Thửa ruộng có S=2180 m2
\(\Rightarrow\frac{a.h}{2}=2180\Rightarrow a.h=4360\Rightarrow a=\frac{4360}{h}\left(1\right)\)
Tăng cạnh 4m ; giảm chiều cao tương ứng 1m thì S không đổi
\(\Rightarrow\left(a+4\right)\left(h-1\right)=4360\left(2\right)\)
Thay (1) vào (2) ; ta được :
\(\left(\frac{4360}{h}+4\right)\left(h-1\right)=4360\)
\(\Leftrightarrow\frac{\left(4360+4h\right)\left(h-1\right)}{h}=\frac{4360h}{h}\)
\(\Leftrightarrow4h^2+4356h-4360-4360h=0\)
\(\Leftrightarrow4h^2-4h-4360=0\)
\(\Delta'=2^2-4.\left(-4360\right)=17444>0\)
\(\Rightarrow\hept{\begin{cases}h_1=\frac{2+\sqrt{17444}}{4}=\frac{1+7\sqrt{89}}{2}\left(TM\right)\\h_2=\frac{2-\sqrt{17444}}{4}=\frac{1-7\sqrt{89}}{2}\left(KTM\right)\end{cases}}\)
Vậy chiều dài một cạnh cần tính là :
\(\frac{4360}{h}=\frac{4360}{\frac{1+7\sqrt{89}}{2}}=-2+14\sqrt{89}\left(m\right)\)

Gọi cạnh đáy của tam giác ban đầu là \(x\left(dm,x>0\right)\)
Vì tam giác ban đầu có chiều cao bằng \(\frac{3}{4}\)cạnh đáy nên chiều cao của tam giác ban đầu là \(\frac{3}{4}x\)
Diện tích của tam giác ban đầu là \(\frac{1}{2}.x.\frac{3}{4}x=\frac{3}{8}x^2\left(dm^2\right)\)
Vì chiều cao tăng thêm 3dm nên chiều cao của tam giác lúc sau là \(\frac{3}{4}x+3\left(dm\right)\)
Cạnh đáy giảm 2dm nên cạnh đáy của tam giác lúc sau là \(x-2\left(dm\right)\)
Diện tích của tam giác lúc sau là \(\frac{1}{2}\left(\frac{3}{4}x+3\right)\left(x-2\right)\left(dm^2\right)\)
Vì diện tích của tam giác lúc sau lớn hơn diện tích tam giác ban đầu là \(12dm^2\)nên ta có phương trình:
\(\frac{1}{2}\left(\frac{3}{4}x+3\right)\left(x-2\right)-\frac{3}{8}x^2=12\)\(\Leftrightarrow\left(\frac{3}{8}x+\frac{3}{2}\right)\left(x-2\right)-\frac{3}{8}x^2=12\)\(\Leftrightarrow\frac{3}{8}x^2-\frac{3}{4}x+\frac{3}{2}x-3-\frac{3}{8}x^2=12\)\(\Leftrightarrow\frac{3}{4}x=15\Leftrightarrow x=20\)(nhận)
Vậy chiều cao của tam giác ban đầu là 15dm, cạnh đáy ban đầu là 20dm.


Gọi chiều cao ứng với cạnh đáy của thửa ruộng là h (m); h > 4
Vì thửa ruộng hình tam giác có diện tích 120 m 2 nên chiều dài cạnh đáy thửa ruộng là 120.2/h hay 240/h (m)
Vì tăng cạnh đáy thêm 5m và chiều cao giảm đi 4m thì diện tích giảm 40 m 2 nên ta có phương trình:
Đáp án B