Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Số photon chiếu tới:
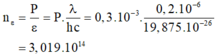
- Số electron bứt ra khỏi Catot:
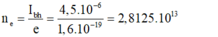
- Hiệu suất lượng tử là:
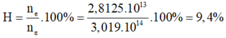

Công suất của chùm phôtôn là \(P = W.t= 0,3.10^{-3}.1=0,3.10^{-3}W.\)
Số phôtôn đến catôt trong 1 s là \(N =\frac{P}{\varepsilon}=\frac{P\lambda}{hc}= \frac{0,3.10^{-3}.0,2.10^{-6}}{6,625.10^{-34}.3.10^8}= 3,02.10^{14}\)
Số electron bật ra từ catôt đến anôt trong 1 s là \(n = \frac{I_{bh}}{|e|}= \frac{4,5.10^{-6}}{1,6.10^{-19}}= 2,812.10^{13}\)
Hiệu suất lượng tử \(H= \frac{n}{N}.100=\frac{2,812.10^{13}}{.3,02.10^{14}}.100= 9,31 \%\)

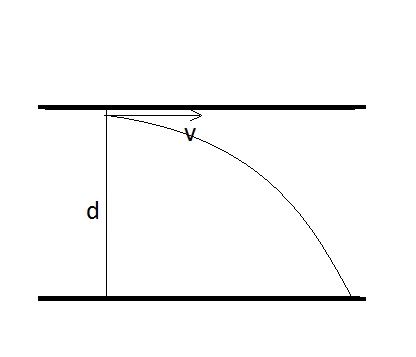
Vận tốc cực đại của electron bắn ra từ catode là \(v\). Ta có:
\(\frac{mv^2}{2}=eU_h\) (\(U_h=2V\) là hiệu điện thế hãm)
\(\Rightarrow v=\sqrt{\frac{2U_he}{m}}=8,4.10^5\text{(m/s)}\)
Vận tốc này có thế theo mọi hướng, để đập vào anode với bán kính lớn nhất thì electron sẽ có vận tốc theo phương song song với bản phẳng.
|
\(t=\sqrt{\frac{2d}{a}}=\sqrt{\frac{2d^2m_e}{U_e}}=2,4.10^{-8}\left(s\right)\)
Bán kính lớn nhất:
\(r=vt=0,02\left(m\right)=2\left(cm\right)\)
\(chọn.A\)

Số electron đến anôt trong 1 s là \(n = \frac{I_{bh}}{|e|}= \frac{3.10^{-6}}{1,6.10^{-19}}=1,875.10^{13}. \)
Hiệu suất lượng tử \(H = \frac{n}{N}.100\)=> Số hạt phôtôn bay đến catôt là
\(N = \frac{n.100}{50}= \frac{1,875.10^{13}.100}{50}= 3,75.10^{13}.\)
Công suất của chùm sáng là
\(P = N.\varepsilon = N\frac{hc}{\lambda}=3,75.10^{13}.\frac{6,625.10^{-34}.3.10^8}{0,36.10^{-6}}= 2,07.10^{-5}W= 20,7.10^{-6}W.\)

a. Bước sóng của chùm sáng: \(\lambda=\dfrac{c}{f}=\dfrac{3.10^8}{10^{15}}=0,3\mu m\)
Giới hạn quang điện: \(\lambda_0=\dfrac{hc}{A_t}=\dfrac{6,625.10^{-34}.3.10^8}{5,15.1,6.10^{-19}}=0,24.19^-6m=0,24\mu m\)
Do \(\lambda > \lambda_0\) nên không xảy ra hiện tượng quang điện.
b. Ta có: \({W_{d0}} = \frac{{hc}}{\lambda } - A = 1,{7.10^{ - 19}}J\Rightarrow {v_0} = \sqrt {\frac{{2{W_{d0}}}}{m}} = 0,{6.10^6}m/s\)
c. \({n_e} = \frac{{{I_{bh}}}}{e} = 2,{8.10^{13}};\,\,\,\,\,\,{n_\lambda } = \frac{P}{{\frac{{hc}}{\lambda }}} = \frac{{P\lambda }}{{hc}} ={3.10^{15}} \Rightarrow H = \frac{{{n_e}}}{{{n_\lambda }}} = 9,{3.10^{ - 3}} = 0,93\% \)



Chọn đáp án A