Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

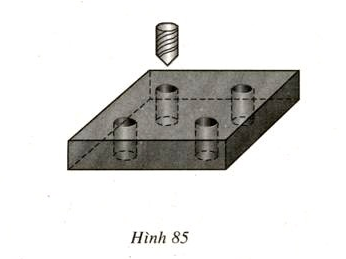
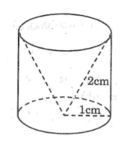
Bán kính đáy của hình trụ (lỗ khoan) là 4mm. Tấm kim loại dày 2cm (20mm) chính là chiều cao của hình trụ.
Thể tích một lỗ khoan hình trụ là:
V 1 = π · 16 . 20 ≈ 1005 mm 3 = 1 , 005 cm 3
Thể tích 4 lỗ khoan bằng:
4. V 1 = 4.1 , 005 = 4 , 02 cm 3
Thể tích tấm kim loại chưa khoan là:
V = 5.5.2 = 50 cm 3
Thể tích còn lại là:
V − 4. V 1 = 50 − 4 , 02 = 45 , 98 cm 3

Giải:
Bán kính đáy của hình trụ (lỗ khoan) 4mm. Tấm kim loại dày 2cm ( 20mm) chính là chiều cao của hình trụ. Thể tích một lỗ khoan hình trụ là V1 = π.16.20 ≈ 1005 (mm3). Thể tích của bốn lỗ khoan là V4 = 4V1 ≈ 4,02 (cm3).
Thể tích của tấm kim loại là:
V = 5.5.2 = 20 (cm2

Bán kính mũi khoan là : \(8:2=4\left(mm\right)=0,4cm\)
Thể tích 4 lỗ khoan dạng hình trụ là :
\(3,14.0,4^2.2.4=4,0192\left(cm^3\right)\)
Thể tích tấm kim loại khi chưa khoan thủng là :
\(5.5.2=50\left(cm^3\right)\)
Thể tích phần còn lại của tấm kim loại là :
\(50-4,0192=45,9808\left(cm^3\right)\)
Vậy ...

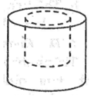
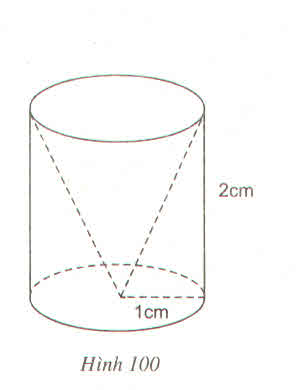
Thể tích vật thể hình trụ : V 1 = π 2 r 2 .2r = 8π r 3 ( c m 3 )
Thể tích lỗ khoan hình trụ : V 2 = π r 2 .r = π r 3 ( c m 3 )
Thể tích vật còn lại : V = V 1 – V 2 = 8π r 3 - π r 3 = 7π r 3 ( c m 3 )
Vậy chọn đáp án B

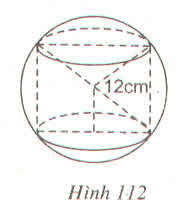
a) Diện tích xung quanh của hình trụ : \(288\pi\left(cm^2\right)\)
b) Thể tích hình cầu : \(2304\pi\left(cm^3\right)\)
c) Diện tích mặt cầu : \(576\pi\left(cm^2\right)\)



 A
.
2
π
3
(
c
m
3
)
B
.
4
π
3
(
c
m
3
)
C
.
2
π
(
c
m
3
)
D
.
8
π
3
(
c
m
3
)
A
.
2
π
3
(
c
m
3
)
B
.
4
π
3
(
c
m
3
)
C
.
2
π
(
c
m
3
)
D
.
8
π
3
(
c
m
3
)

Bán kính đáy của hình trụ (lỗ khoan) là 4mm. Tấm kim loại dày 2cm (20mm) chính là chiều cao của hình trụ.
Thể tích một lỗ khoan hình trụ là:
V1 = π.16.20 ≈ 1005 (mm3) = 1,005 (cm3).
Thể tích 4 lỗ khoan bằng:
4.V1 = 4.1,005 = 4,02 (cm3).
Thể tích tấm kim loại chưa khoan là:
V = 5.5.2 = 50 (cm3)
Thể tích còn lại là:
V – 4.V1 = 50 – 4,02 = 45,98 (cm3).