Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
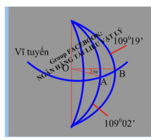
+ Ta có khoảng cách giữa đài VTV và vệ tinh là d = h 2 + x 2
Với h = R sin ( 21 0 ) = 6400 sin ( 21 0 ) ≈ 2294 k m
x = R cos 21 0 2 + R + h 2 − 2 R cos 21 0 R + h cos 27 0
Vậy d = h 2 + x 2 = 2294 2 + 36998 2 = 37069 k m
→ Thời gian sóng truyền giữa hai vị trí trên t = d c = 37069.10 3 3.10 8 = 124 m s

Chọn đáp án B
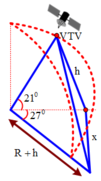
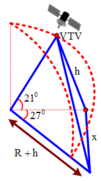
+ Ta có khoảng cách giữa đài VTV và vệ tinh là d = h 2 + x 2
Với h = R sin ( 21 0 ) = 6400 sin ( 21 0 ) ≈ 2294 k m
x = R cos 21 0 2 + R + h 2 − 2 R cos 21 0 R + h cos 27 0
Vậy d = h 2 + x 2 = 2294 2 + 36998 2 = 37069 k m
→ Thời gian sóng truyền giữa hai vị trí trên t = d c = 37069.10 3 3.10 8 = 124 m s

Do E và B biến thiên cùng pha, cùng tần số nên:
\(\dfrac{E}{E_0}=\dfrac{B}{B_0}\Rightarrow \dfrac{4}{10}=\dfrac{B}{0,2}\)
\(\Rightarrow B = 0,08 T\)
Áp dụng quy tắc vEB với ngón cái, trỏ, ngón giữa theo thứ tự là v, E, B ta thấy B hướng xuống.

Vận tốc cực đại: \(v_{max}=\sqrt{\dfrac{2W_{đmax}}{m}}=\sqrt{\dfrac{2.0,1}{0,2}}=1m/s\)
Khi \(W_{đ1}=0,025J\) \(\Rightarrow v_{1}=\sqrt{\dfrac{2W_{đ1}}{m}}=\sqrt{\dfrac{2.0,025}{0,2}}=0,5m/s\)
Khi \(W_{đ2}=0,75J\) \(\Rightarrow v_{1}=\sqrt{\dfrac{2W_{đ1}}{m}}=\sqrt{\dfrac{2.0,075}{0,2}}=0,5\sqrt 3m/s\)
Vì vận tốc biến thiên điều hoà theo thời gian, nên ta biểu diễn bằng véc tơ quay:
v O 1 0,5 0,5√3 30 0
Từ giản đồ véc tơ ta suy ra được: \(\Delta t=\dfrac{30}{360}T=\dfrac{\pi}{20}\)
\(\Rightarrow T =\dfrac{3\pi}{5}s\)
\(\Rightarrow \omega = \dfrac{2\pi}{T}=\dfrac{10}{3}\) (rad/s)
Biên độ: \(A=\dfrac{v_{max}}{\omega}=0,3m = 30cm\)

Hai điểm có cùng biên độ 2 mm đối xứng nhau qua nút gần nhất và hai điểm có biên độ 3 mm nằm đồi xứng nhau qua bụng gần nhất. Áp dụng công thức tình biên độ điểm, ta có hệ phương trình:
Gọi biên độ sóng tại bụng là 2a.
Ta có : \(\frac{1}{a^2}=\frac{9}{4a^2}=1\rightarrow a=\frac{2}{\sqrt{13}}\)
Xét: \(2a\sin\frac{2\pi x}{\lambda}=2\rightarrow2\lambda=54cm\Rightarrow\lambda=27cm\)
Vậy chọn đáp án A.