Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Trạng thái đầu:
V 1 = 40 c m 3 ; p 1 = 75 – 8 = 67 cmHg.
Trạng thái cuối: V 2 c m 3 ; p 2 = 75 cmHg.
Vì nhiệt độ không đổi nên ta có:
p 1 V 1 = p 2 V 2 → V 2 = p 1 V 1 / p 2 ≈ 35 , 7 c m 3

Chọn D.
Trạng thái đầu: V1 = 40 cm3; p1 = 75 – 8 = 67 cmHg.
Trạng thái cuối: V2 cm3; p2 = 75 cmHg.
Vì nhiệt độ không đổi nên ta có: pV1 = p2V2 → V2 = p1V1/p2 ≈ 35,7 cm3

Chọn D.
Trạng thái đầu:
V 1 = 40 c m 3 ; p 1 = 75 – 8 = 67 cmHg.
Trạng thái cuối: V 2 c m 3 ; p 2 = 75 cmHg.
Vì nhiệt độ không đổi nên ta có:
p V 1 = p 2 V 2 → V 2 = p 1 V 1 / p 2 ≈ 35,7 c m 3

Gọi S là diện tích ống thủy tinh.
Chiều dài cột không khí có trong ống là l1 = 60 – 40 = 20 cm.
Áp suất không khí trong ống p 1 = p 0 + 40 = 120 ( c m H g )
Khi lật ngược miệng ống phía dưới thì cột thủy ngân còn lại trong ống là x nên p 2 = p 0 − x = 80 − x ( c m H g ) chiều dài cột không khí l2 = 60 – x
Ta có
p 1 V 1 = p 2 V 2 ⇒ p 1 . l 1 . S = p 2 . l 2 . S ⇒ 120.20 = ( 80 − x ) ( 60 − x ) ⇒ x 2 − 140 x + 2400 = 0 ⇒ { x 1 = 120 ( c m ) x 2 = 20 ( c m )
Mà x < 40 c m nên x = 20 ( cm )
Vậy độ cao cột thủy ngân còn lại trong ống là 20 cm

Đáp án C
Gọi p 1 và p lần lượt là áp suất của không khí trong ống ở nhiệt độ T o và T:
![]()
Áp dụng phương trình trạng thái cho lượng khí trong ống
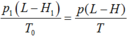
Từ đó rút ra: 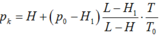

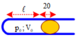
Gọi S là diện tích ống thủy tinh. Chiều dài cột không khí có trong ống là

Khi lật ngược miệng ống phía dưới thì cột thủy ngân còn lại trong ống là x nên
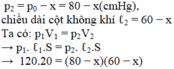
Mà x < 40(cm) nên x = 20(cm)
Vậy độ cao cột thủy ngân còn lại trong ống là 20cm

Ban đầu, chiều dài không khí hai bên cột thủy ngân là: (100 - 20) / 2 = 40cm.
Khi dựng đứng ống thủy tinh, cột thủy ngân dịch xuống 1 đoạn x(cm), khi đó:
- Chiều dài cột không khí ở trên: 40 + x,
- Chiều dài cột không khí ở dưới là: 40 - x
Áp suất ở trên là P1, ở dưới là P2 thì: P2 = P1 + 20 (tính theo cmHg)
Mặt khác, quá trình đẳng nhiệt ta có:
\(\dfrac{P_1}{P_0}=\dfrac{V_0}{V_1}=\dfrac{40}{40+x}\)\(\Rightarrow P_1=\dfrac{40}{40+x}P_0\)(1)
\(\dfrac{P_2}{P_0}=\dfrac{V_0}{V_2}=\dfrac{40}{40-x}\)\(\Rightarrow P_2=\dfrac{40}{40-x}P_0\)(2)
Suy ra: \(P_2-P_1=P_0(\dfrac{40}{40-x}-\dfrac{40}{40+x})=P_0.40.\dfrac{2x}{40^2-x^2}\)
\(\Rightarrow 20=50.40.\dfrac{2x}{40^2-x^2}\)
\(\Rightarrow x = 7,7cm\)
Thay vào (1) và (2) ta sẽ tìm đc P1 và P2
![]()

Trạng thái 1 của mỗi lượng khí ở hai bên cột thủy ngân (ống nằm ngang)
p 1 ; V 1 = (L - h)/2 . S; T 1
Trạng thái 2 (ống thẳng đứng)
+ Đối với lượng khí ở trên cột thủy ngân: p 2 ; V 2 = ((L - h)/2 + 1).S; T 2 = T 1
+ Đối với lượng khí ở dưới cột thủy ngân: p ' 2 ; V ' 2 = ((L - h)/2 + 1).S; T ' 2 = T 1
Áp suất khí ở phần dưới bằng áp suất khí ở phần trên cộng với áp suất do cột thủy ngân gây ra. Do đó đối với khí ở phần dưới, ta có:
p ' 2 = p 2 + h; V ' 2 = ((L - h)/2 + 1).S; T ' 2 = T 1
Áp dụng định luật Bôi-lơ – Ma-ri-ốt cho từng lượng khí. Ta có:
+ Đối với khí ở trên:
p 1 (L - h)S/2 = p 2 (L - h + 2l)S/2
⇒ p 1 (L - h) = p 2 (L - h + 2l) (1)
+ Đối với khí ở dưới:
p 1 (L - h)S/2 = ( p 2 + h)(L - h + 2l)S/2
⇒ p 1 (L - h) = ( p 2 + h)(L - h + 2l) (1)
Từ hai phương trình (1) và (2) rút ra:
p 2 = h(L - h - 2l)/4l
Thay giá trị của p2 vào (1) ta được:
p 1 = 37,5(cmHg)
p 1 = ρ gH = 1,36. 10 4 .9,8.0,375 = 5. 10 4 Pa.

Do có hiện tượng mao dẫn nên thủy ngân trong ống thủy tinh bị tụt xuống một đoạn:
![]()
Áp suất thực của khí quyển tại vị trí đo là p = 760 + 9,8 = 769,8mmHg.
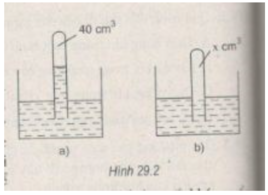
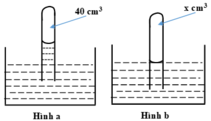
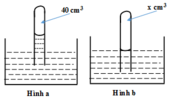
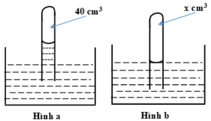

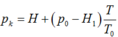
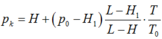
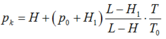
Trạng thái đầu: V 1 = 40 c m 3 ; p 1 = 75 – 8 = 67 cmHg.
Trạng thái cuối: V 2 = ? c m 3 ; p 2 = 75 cmHg.
Vì nhiệt độ không đổi nên: p 1 V 1 = p 2 V 2
⇒ V 2 = p 1 V 1 / p 2 ≈ 35,7( c m 3 )