Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có g → / = g → + a → q t mà trọng lượng của vật khi thang máy chuyển động là P / = m g /
a. Khi thang máy đứng yên a = 0 m / s 2
⇒ N = P = m g = 10.10 = 100 N
b. Đi lên nhanh dần đều với gia tốc 1 m / s 2
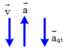
a → q t ↓ ↓ g → ⇒ g / = g + a q t
⇒ g / = 10 + 2 = 12 m / s 2 ⇒ N = P / = m g / = 10.12 = 120 N
c. Đi lên chậm dần đều với gia tốc 2 m / s 2
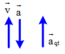
a → q t ↑ ↓ g → ⇒ g / = g − a q t
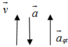
⇒ g / = 10 − 2 = 8 m / s 2 ⇒ N = P / = m g / = 10.8 = 80 N
d. Đi xuống nhanh dần đều với gia tốc 2 m / s 2
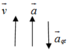
a → q t ↑ ↓ g → ⇒ g / = g − a q t
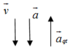
⇒ g / = 10 − 2 = 8 m / s 2 ⇒ N = P / = m g / = 10.8 = 80 N
e. Đi xuống chậm dần đều với gia tốc 2 m / s 2
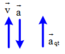
a → q t ↓ ↓ g → ⇒ g / = g + a q t
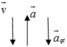
⇒ g / = 10 + 2 = 12 m / s 2 ⇒ N = P / = m g / = 10.12 = 120 N
f. Chuyển động thẳng đều 2m/s
Vì thang máy chuyển động thẳng đều nên
a = 0 m / s 2 ⇒ N = P = m g = 10.10 = 100 N

Hướng của gia tốc trọng trường là \(g\)có chiều đi xuống dưới.
Khi thang đi lên, hướng \(a\)đi lên trên nên gia tốc là: \(g+a\).
Khi thang đi xuống hướng \(a\)đi xuống dưới nên gia tốc là: \(g-a\).

Xem hệ hai xe là hệ cô lập
- Áp dụng địmh luật bảo toàn động lượng của hệ.
\(m_1=v_1=\left(m_1+m_2\right)\overrightarrow{v}\)
\(\overrightarrow{v}\)cùng phương với vận tốc \(\overrightarrow{v_1}\)
Vận tốc của mỗi xe là:
\(v=\frac{m_1.v_1}{m_1+m_2}=1,45\left(m\text{/}s\right)\)