Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Chọn 1 quân bài từ cỗ 1, có 52 cách
Chọn 1 quân bài từ cỗ 2, có 52 cách
Chọn 1 quân bài từ cỗ 3, có 52 cách
$\Rightarrow$ tổng có $52^3$ cách
Chọn 1 quân bài bất kỳ từ cỗ 1, có 52 cách. Chọn 1 quân bài từ cỗ 2 mà không trùng chất với cỗ 1, có $52-13=39$ cách. Chọn 1 quân bài từ cỗ 3 mà không trùng chất với cỗ 1,2, có $39-13=26$ cách.
Số cách chọn 3 quân bài không trùng chất: $52.39.26$ (cách)
Xác suất: $\frac{52.39.26}{52^3}=\frac{3}{8}$

y ' = - 3 x 2 + 2 ( 2 m + 1 ) x - m 2 + 3 m - 2
Để hàm số đã cho có cực đại, cực tiểu nằm về hai phía so với trục tung khi và chỉ khi phương trình y’ = 0 có hai nghiệm x 1 , x 2 trái dấu.
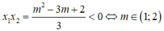
Chọn A
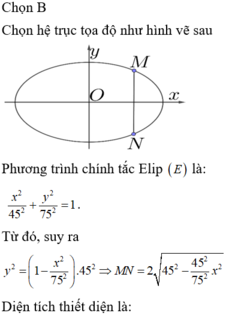




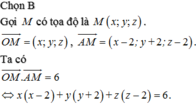
Để trục xe đạt yêu cầu, đường kính phải nằm trong khoảng từ 1,25 - 0,2 = 1,05 cm đến 1,25 + 0,2 = 1,45 cm.
Xác suất để đường kính trục xe nằm ngoài khoảng này được tính bằng diện tích phía ngoài khoảng chia cho tổng diện tích của phân phối chuẩn:
P(X < 1,05 cm or X > 1,45 cm) = P(X < 1,05 cm) + P(X > 1,45 cm)
Trong đó X là đường kính trục xe và được mô tả bởi phân phối chuẩn với độ lệch chuẩn σ = 0,01 mm.
Chuyển đổi đơn vị đường kính thành cm:
σ = 0,01 mm = 0,001 cm
Tìm xác suất cho giá trị X nhỏ hơn 1,05 cm:
Z = (1,05 - 1,25) / 0,001 = -200
P(X < 1,05 cm) = P(Z < -200) ≈ 0
Tương tự, tìm xác suất cho giá trị X lớn hơn 1,45 cm:
Z = (1,45 - 1,25) / 0,001 = 200
P(X > 1,45 cm) = P(Z > 200) ≈ 0
Vậy,
P(X < 1,05 cm or X > 1,45 cm) = 0 + 0 = 0
Do đó, xác suất để trục xe không đạt yêu cầu là 0.