K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

AH
Akai Haruma
Giáo viên
20 tháng 12 2016
Có \(I_0=\frac{U}{Z_C}\sqrt{2}=2\sqrt{2}\left(A\right)\)
Vì mạch chỉ có tụ điện $C$ nên cường độ dòng điện tức thời nhanh pha hơn điện áp tức thời một góc $\frac{\pi}{2}$
$\Rightarrow$ biểu thức: \(i=2\sqrt{2}\cos\left(100\pi t+\frac{\pi}{2}\right)\left(A\right)\), tức đáp án $A$ là đáp án đúng

CN
1 tháng 1 2017
\(i=2cos\left(100\pi t-\frac{3\pi}{4}\right)\)
\(\varphi=\varphi_u-\varphi_i=\frac{3\pi}{4}\Rightarrow tan\varphi=-1\)
nên mạch có tính dung kháng suy ra mạch gồm R và C
ta có \(tan\varphi=\frac{-Z_c}{R}=-1\Rightarrow Z_c=R\)(1)
lại có \(Z=\sqrt{R^2+Z_C^2}=\frac{U}{I}=50\)(2)
từ 1,2 suy ra R=Zc=5 \(\Omega\)
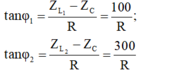
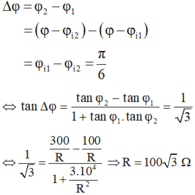
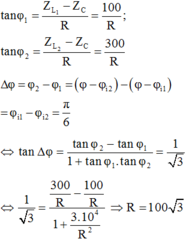



Ta có: \(Z_L=L\omega=100\left(\Omega\right)\)
\(Z_C=\dfrac{1}{C\omega}=200\left(\Omega\right)\)
\(\Rightarrow Z=\sqrt{\left(R+r\right)^2+\left(Z_L-Z_C\right)^2}=100\sqrt{2}\left(\Omega\right)\)
Có: \(U_0=I_0.Z=200\sqrt{2}\left(V\right)\)
\(\tan\varphi=\dfrac{Z_L-Z_C}{R+r}=-1\) \(\Rightarrow\varphi=-\dfrac{\pi}{4}=\varphi_u-\varphi_i\) \(\Rightarrow\varphi_u=-\dfrac{5\pi}{12}\)
Vậy: \(u=200\sqrt{2}\cos\left(100\pi t-\dfrac{5\pi}{12}\right)\)
→ Đáp án: C
Bạn tham khảo nhé!