Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi R 0 là điện trở của quang điện trở trong tối. Ta có
![]()
Gọi R là điện trở của quang điện trở được chiếu sáng. Ta có
I = 0,5A ⇒ R = 20Ω

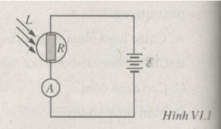
Gọi R Q , R N và r lần lượt là điện trở của quang điện trở (khi được chiêu sáng), của nam châm điện và của nguồn điện, E là suất điện động cùa nguồn. Ta có
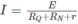
với I ≥ 30mA; R Q = 50 Ω; ; R N = 10 Ω và r ≈ 0, ta được:
E ≥ 1,8V
Khi quang điện trở không được chiếu sáng thì R Q = 3MΩ và I < 30mA. Ta có thêm điều kiện : E < 9. 10 4 V. Điều kiện này đương nhiên đạt được.

Khi quang điện trở không được chiếu sáng :
![]()
Khi quang điện trở được chiếu sáng :
![]()

Chọn đáp án C
Cường độ dòng điện qua quang điện trở là I = U / R . Khi tăng cường độ sáng chiếu vào quang điện trở thì do hiện tượng quang điện trong làm điện trở R giảm. Nên I tăng.
STUDY TIP |
Quang điện trở hoạt động dựa trên hiện tượng quang điện trong, khi cường độ ánh sáng chiếu vào càng lớn thì số hạt tải điện trọng bán dẫn càng lớn tính dẫn điện càng tốt tức là điện trở của nó giảm. |

Khi dung kháng là $100 \Omega$ thì công suất tiêu thụ của đoạn mạch là cực đại bằng 100 W nên
\(\begin{cases} Z_L=Z_{C_1}=100 \Omega \\ P=\dfrac{U^2}{R} =100 W \end{cases}\)
Khi dung kháng là $200 \Omega$ thì điện áp hiệu dụng giữa hai đầu tụ điện là $100\sqrt{2} V$ nên
$U_{C_2}=\dfrac{U.Z_{C_2}}{Z}=\dfrac{200.U}{\sqrt{R^2+(100-200)^2}}=100\sqrt{2}$
$\Rightarrow 2U^2=R^2+100^2$
$\Rightarrow 2.100.R =R^2 +100^2$
$\Rightarrow R=100 \Omega$

Đáp án C.
Lời giải chi tiết:
Cường độ dòng điện qua quang điện trở là I = U/R. Khi tăng cường độ sáng chiếu vào quang điện trở thì do hiện tượng quang điện trong làm điện trở R giảm. Nên I tăng.

Gọi $R_0,Z_L,Z_C$ là các thông số của quạt
Theo bài ra ta có $P_{đm}=120 W $, Dòng điện định mức của quạt là $I$
Gọi $R_2$ là giá trị của biến trở khi quạt hoạt động bình thường khi $U=220V$
Khi $R_1=70.\Omega $ thì $I_1=0,75 A,P_1=0,928P=111,36W$
$P_1=I_1^2.R_0$
$\Rightarrow R_0=\dfrac{P_1}{I_1^2}=198\Omega $
Ta có $I_1=\dfrac{U}{Z_1}=\dfrac{U}{\sqrt{\left(R_0+R_1\right)^2+\left(Z_L-Z_C\right)^2}}=\dfrac{220}{\sqrt{268^2+\left(Z_L-Z_C\right)^2}}$
$\Rightarrow \left(Z_L-Z_C\right)^2=119^2$
Ta lại có
$P=I^2.R_0$
Với $I=\dfrac{U}{Z}=\dfrac{U}{\sqrt{\left(R_0+R_1\right)^2+\left(Z_L-Z_C\right)^2}}$
$\Rightarrow P=\dfrac{U^2}{\left(R_0+R_2\right)^2+\left(Z_L-Z_C\right)^2}$
$\Rightarrow R_0+R_2=256\Omega $
$\Rightarrow R_2=58\Omega $
$R_2 < R_1$
$\Rightarrow \Delta. R=R_1-R_2=12\Omega $
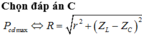
Chọn A