

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Hướng dẫn: Chọn đáp án C
Khoảng thời gian để điện áp u trên tụ có độ lớn u không vượt quá 0 , 8 U 0 trong một chu kì là 4 t 1 = 4 1 ω arcsin 0 , 8 U 0 U 0
Thay số vào ta được: 4 1 ω arcsin 0 , 8 = 4.10 − 6 ⇒ ω ≈ 0 , 93.10 6 (rad/s)

Chọn đáp án C
Khoảng thời gian để điện áp u trên tụ có độ lớn u không vượt quá 0 , 8 U 0 trong một chu kì là 4 t 1 = 4 1 ω arcsin 0 , 8 U 0 U 0
Thay số vào ta được: 4 1 ω arcsin 0 , 8 = 4.10 − 6 ⇒ ω ≈ 0 , 93.10 6 (rad/s)

Chọn đáp án C
Khoảng thời gian để điện áp u trên tụ có độ lớn u không vượt quá 0,8 U 0 trong một chu kì là 4 t 1 = 4 1 ω arcsin 0,8 U 0 U 0
Thay số vào ta được: 4 1 ω arcsin 0,8 = 4.10 − 6 ⇒ ω ≈ 0,93.10 6 (rad/s)

Đáp án D
Phương pháp: Sử dụng̣ vòng tròn lượng̣ giác và công thức tính thời gian
Cách giải:
Thời điểm điện áp trên tụ |u| ≤ 0,8U0 được biểu diễn bằng phần tô đậm như hình vẽ.
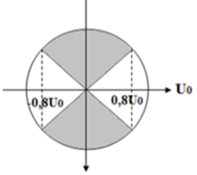 |
Từ đó ta xác định được góc quét của phần tô đậm trong 1 chu kì là α = 3,71rad
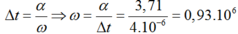 ( rad)
( rad)

Từ ĐK đầu bài ta có:
tần số dao động riwwng của mạch là:
giải phương trình bâc 2 này ra ta được:

\(T = 2\pi .\sqrt{LC} = 2.10^{-5}s.\)
Thời gian từ lúc hiệu điện thế trên tụ cực đại U0 đến lúc hiệu điện thế trên tụ \(+\frac{U_0}{2}\) tính dựa vào đường tròn
U 0 +U 0 2
\(\cos \varphi = \frac{U_)/2}{U_0}= \frac{1}{2}=> \varphi= \frac{\pi}{3}. \)
\( t = \frac{\varphi}{\omega}= \frac{\pi/3}{2\pi/T}= \frac{T}{6}= \frac{1}{3}.10^{-5}s.\)