Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tia đỏ có tia ló đối xứng qua mặt phân giác --> Tia đỏ có góc lệch cực tiểu, khi đó, bạn vẽ hình ra sẽ tìm được góc tới i1
sin i1 / sin 300 = căn 2 --> i1 = 450.
Sau đó, áp dụng công thức thấu kính để tìm góc r2, bạn sẽ thấy xảy ra phản xạ toàn phần với một phần tia sáng --> Tia màu tím không ló ra được
--> Đáp án A sai.

Góc lệch ∆D giữa tia đỏ và tia tím :
∆D = (nt -nđ)A = (1,685 - 1,643).5° =.0,21° = 12,6'

Chọn đáp án C.
δ = ( n t − n d ) A = ( 1 , 68 − 1 , 62 ) 6 0 = 0 , 36 0 ⇔ 0 , 006 ( r a d ) .

A M H Đ T 2m Đ đỏ Đ tím
Góc lệch của tia sáng qua lăng kính khi góc chiết quang nhỏ: \(D=(n-1).A\)
Bề rộng của dải màu trên màn: \(ĐT=HĐ-HT=MH\tanĐ_{tím}-MH\tanĐ_{đỏ}=MH(\tanĐ_{tím}-\tanĐ_{đỏ})\)
Do góc lệch Đ nhỏ nên \(\tan Đ = Đ_{(tính- theo- rad)}\)
\(\Rightarrow ĐT = MH(Đ_{tím}-Đ_{đỏ})=MH.(n_t-n_đ).A=2.(1,54-1,5).(6.60.3.10^{-4})=0,00864m=8,64mm\)

a/ Chiết suất của lăng kính đối với tia tím và đỏ tính theo (1) là:
\(n_t=1,7311\text{≈}\sqrt{3};\)\(n_đ=1,4142\text{≈}\sqrt{2}\)
Khi góc lệch của tia tím là cực tiểu thì: \(\iota'_1=\iota_2\Rightarrow r_1=r_2=\frac{A}{2}\)
và \(D_{min}=2\iota_1-A\) hay \(\iota_1=\frac{D_{tmin}+A}{2}\)
áp dụng công thức : \(\sin\iota_1=n\sin r_1\) ta được \(\sin D_{tmin}+A_2=n_t\sin\frac{A}{2}\)
Đối với tia tím \(n_t=\sqrt{3}\) và biết \(A=60^0\), ta được:
\(\sin D_{tmin}+A_2=60^0\Rightarrow D_{tmin}=60^0\)
Góc tới của tia sáng trắng ở mặt AB phải bằng:\(i_t=60^0\)
b/ Tương tự như vậy, muốn cho góc lệch của tia đỏ là cực tiểu thì:
\(\sin\frac{D_{dmin}+A}{2}=n_d\sin\frac{A}{2}\Rightarrow D_{dmin}=30^0\)
và góc tới của tia sáng trắng trên mặt AB là: \(i_đ=45^0\)
Như vậy phải giảm góc tới trên mặt AB một góc là :\(i_t-t_đ=15^0\), tức là phải quay lăng kính quanh cạnh A một góc \(15^0\) ngược chiều kim đồng hồ.
c/Gọi \(r_{0đ}\)và \(r_{0t}\) là các góc giới hạn phản xạ toàn phần của tia đỏ và tia tím ta có:
\(\sin r_{0đ}=\frac{1}{n_d}=\frac{1}{\sqrt{2}}\Rightarrow r_{0đ}=45^0\)
\(\sin r_{0t}=\frac{1}{n_t}=\frac{1}{\sqrt{3}}\)=>r0t < r0đ .Do đó muốn cho không có tia sáng nào ló ra khỏi mặt AC của lăng kính thì phải có: r2 \(\ge\)r0đ \(\Rightarrow r_2\ge15^0\)
Hay \(\sin r_1\ge\sin\left(60^0-45^0\right)=0,2588\)
Biết \(\sin r_{1t}=\frac{\sin\iota}{n_t},\sin r_{1đ}=\frac{\sin\iota}{n_d}\); vì \(n_t\le n_đ\)nên suy ra \(r_{1t}\le\sin r_{1đ}\)(2)
Từ (1) và (2) ta thấy bất đẳng thức (1) được thõa mãn đối với mọi tia sáng, nghĩa là không có tia nào trong chùm sáng trắng ló ra khỏi mặt AC, nếu
\(\sin r_{1đ}\le0,2588\)hay \(\frac{\sin\iota}{n_đ}<0,2588\)
\(\Rightarrow\sin i\le0,2588.n_đ\)\(\Rightarrow\sin\le0,36\) .Suy ra góc tới:\(i\le21^06'\)

Chọn đáp án A
Áp dụng công thức lăng kính: S i n i 1 = n . sin r 1 S i n i 2 = n . sin r 2 r 1 + r 2 = A D = ( i 1 + i 2 ) − A
+ Đối với tia đỏ: s i n i 1 = n d . sin r 1 d ⇒ sin r 1 d = sin 60 0 n d ⇒ r 1 d = 34 , 22 0 r 1 d + r 2 d = A ⇒ r 2 d = A − r 1 d = 15 , 78 0 s i n i 2 d = n . sin r 2 d ⇒ sin r 2 d = n d sin r 2 d ⇒ i 2 d = 24 , 76 0 D = ( i 1 + i 2 d ) − A = 60 0 + 24 , 76 0 − 50 0 = 34 , 76 0
+ Đối với tia tím: s i n 60 0 = n t . sin r 1 t ⇒ r 1 t = 33 , 24 0 r 1 t + r 2 t = A ⇒ r 2 t = A − r 1 t = 16 , 76 0 s i n i 2 t = n . sin r 2 t ⇒ sin r 2 t = n t sin r 2 t ⇒ i 2 t = 27 , 1 0 D = i 1 + i 2 d − A = 60 0 + 27 , 1 0 − 50 0 = 37 , 1 0
+ Góc hợp bởi giữa hai tia đỏ và tia tím sau khi ló ra khỏi lăng kính: D t - D d = 2 , 34 °

Góc lệch của tia ló chính là góc lệch so với phương của tia tới, và nó là D nhé.
\(D=\left(n-1\right)A\) (Công thức này đúng khi góc chiết quang nhỏ hơn 100, là góc nhỏ)
Vận tốc của tia sáng trong môi trường chiết suất n là: \(v=\frac{3.10^8}{n}\Rightarrow n=\frac{3}{1,98}\)
Mình ra là 0,0834 rad :P
b cho t hỏi cái 1'=3*10^-4 thì áp dụng như thế nào vậy. t cảm ơn nhiều

Bạn click vào câu hỏi tương tự ở trên nhé, có nhiều câu tương tự lắm
Góc lệch của tia sáng khi qua lăng kính trong trường hợp góc chiết quang nhỏ là: \(D = (n-1)A\)
\(\Rightarrow D_đ=(n_đ-1)A\)
\(D_t=(n_t-1)A\)
Suy ra \(\Delta D = D_t-D_đ=(n_t-n_đ)A\)
Bạn thay số nhế
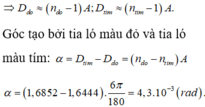
Đáp án B
+ Góc lệch qua lăng kính với trường hợp góc tới nhỏ D = A(n – 1) → ΔD = A(nt – nd) = 0,0044 rad.