Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu là số cách chọn ngẫu nhiên 5 viên bi từ hộp chứa 18 viên bi.Suy ra số phần tử của không gian mẫu là Ω = C 18 5 = 8568
Gọi A là biến cố "5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng". Ta có các trường hợp thuận lợi cho biến cố A là:

Chọn A

\(\Omega\) lấy 3 viên bi
\(\left|\Omega\right|=C^3_{12}\)
gọi A" 3 viên lấy ra màu đỏ"
\(\left|A\right|=C^3_7\)
Suy ra
\(P\left(A\right)=\frac{C^3_7}{C^3_{12}}\)

Chọn B.
Số cách lấy 7 viên bi từ hộp là C 35 7
Số cách lấy 7 viên bi không có viên bi đỏ là C 20 7 .
Số cách lấy 7 viên vi có ít nhất 1 viên đỏ là C 55 7 - C 20 7 xác suất là C 55 7 - C 20 7 C 55 7 .

Đáp án A
Lấy ngẫu nhiên 3 viên bi trong 12 viên bi có C 12 3 = 220 cách ⇒ n Ω = 220 .
Gọi X là biến cố “3 bi được chọn có đủ 3 màu”
Lấy 1 viên bi màu đỏ trong 3 bi đỏ có 3 cách.
Lấy 1 viên bi màu xanh trong 4 bi xanh có 4 cách.
Lấy 1 viên bi màu vàng trong 5 bi vàng có 5 cách.
Suy ra số kết quả thuận lợi cho biến cố X là n X = 3 . 4 . 5 = 60 . Vậy P = n X n Ω = 3 11 .


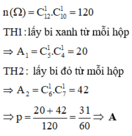
C
Số phần tử của không gian mẫu chính là số
cách lấy ngẫu nhiên 6 viên bi bất kì trong 18
viên nên n Ω = C 18 6
Gọi A là biến cố “6 bi lấy được có đủ ba màu
đồng thời hiệu của số bi đỏ và trắng, hiệu của
số bi xanh và đỏ, hiệu của số bi trắng và xanh
theo thứ tự lập thành cấp số cộng”
Gọi t, d, x lần lượt là số bi trắng,bi đỏ và bi xanh
trong 6 viên bi được chọn ra.
Theo bài ta có: d − t , x − d , t − x
lập thành một cấp số cộng.
Do đó: d − t + t − x = 2 x − d ⇔ d = x .
Lại có t+d+x=6 nên ta có các trường hợp.
Trường hợp 1. d = x = 1 và t = 4. Khi đó số cách chọn 6 viên bi là C 6 1 C 7 1 C 5 4 = 210 cách.
Trường hợp 2. t = d = x = 2. Khi đó số cách chọn 6 viên bi là C 6 2 C 7 2 C 5 2 = 3150 cách.
Vậy số phần tử của biến cố A là n A = 210 + 3150 = 3360
Do đó xác suất của biến cố A là P A = n A n Ω = 3360 C 18 6 = 40 221