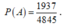Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Số phần tử của không gian mẫu là: ![]() .
.
Gọi A là biến cố “chọn được 4 đại biểu sao cho mỗi Quốc gia đều có ít nhất 1 đại biểu và có cả đại biểu nam và nữ.”
Trường hợp 1: có 2 đại biểu Việt Nam, 1 đại biểu Mỹ, 1 đại biểu Anh.
Số cách chọn ra 4 đại biểu có cả đại biểu nam và đại biểu nữ thỏa mãn trường hợp 1 là: ![]() cách chọn.
cách chọn.
Trường hợp 2: Có 1 đại biểu Việt Nam, 2 đại biểu Mỹ,1 đại biểu Anh.
Số cách chọn ra 4 đại biểu có cả đại biểu nam và đại biểu nữ thỏa mãn trường hợp 2 là:![]()
Trường hợp 3: Có 1 đại biểu Việt Nam, 1 đại biểu Mỹ, 2 đại biểu Anh.
Số cách chọn ra 4 đại biểu có cả đại biểu nam và đại biểu nữ thỏa mãn trường hợp 3 là: ![]() .
.
Nên tổng số cách chọn thỏa mãn yêu cầu là: 581 + 678 + 678 = 1937.
Vậy xác suất của biến cố A là: ![]() .
.

Không gian mẫu: \(7!\)
Hoán vị 3 đại biểu nam: 3! cách
3 đại biểu nam tạo ra 4 khe trống, xếp 4 đại biểu nữ vào 4 khe trống: \(A_4^4\) cách
Xác suất: \(P=\dfrac{3!.A_4^4}{7!}=...\)

Số cái bắt tay ít nhất đã xảy ra là \(C^2_{20}=20\cdot19:2=190\left(cái\right)\)

a/ Chọn 4 đại biểu từ 4 nước, mỗi nước một đại biểu, có \(4.4.4.4=256\) cách
Còn lại 2 đại biểu chọn bất kì từ 12 đại biểu còn lại: \(C_{12}^2=66\) cách
Vậy có \(256.66=...\) cách
b/
Số cách chọn mỗi đoàn có ko nhiều hơn 2 đb, trong đó 1 đoàn ko có đb nào: \(3.\left(C_4^2\right)^3=...\)
Số cách chọn mỗi đoàn có ko nhiều hơn 2 đb, trong đó đoàn nào cũng có đb: \(4^3\left(C_{12}^2-3.C_4^2\right)=...\)
Số cách chọn thỏa mãn: \(3.\left(C_4^2\right)^3+4^3\left(C_{12}^2-3.C_4^2\right)=...\)

- Đếm số cách để A và B ngồi cạnh nhau, C ngồi vị trí bất kì:
Coi A, B là một người, có \(2!\) cách xếp vị trí A, B.
Khi đó ta xếp vị trí của 9 người: \(9!\).
Có tổng số cách xếp là: \(2!.9!\).
- Đếm số cách để A và B ngồi cạnh nhau, C ngồi cạnh A.
Coi A, B, C là một người. Có 2 cách xếp thỏa mãn là CAB, BAC.
Khi đó ta xếp vị trí của \(8\) người: \(8!\).
Có số cách xếp là: \(2.8!\).
Vậy số cách xếp để A và B ngồi cạnh nhau, A và C không ngồi cạnh nhau là \(2!.9!-2.8!\).

Đáp án A
Số cách chọn 1 người trong 20 người làm trưởng đoàn là: C 20 1 cách.
Số cách chọn 1 người trong 19 người còn lại làm phó đoàn là: C 19 1 cách.
Số cách chọn 1 người trong 18 người còn lại làm thư kí là: C 18 1 cách.
Số cách chọn 3 người trong 17 người còn lại làm ủy viên là: C 17 3 cách.
Vậy số cách chọn đoàn đại biểu là C 20 1 . C 19 1 . C 18 1 . C 17 3 = 4651200 .

Chọn B
Số phần tử của không gian mẫu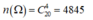
Gọi A là biến cố: “chọn được 4 đại biểu để trong đó mỗi nước đều có 1 đại biểu và có cả đại biểu
nam và đại biểu nữ”
Số cách chọn 4 người đủ các nước tức là có một nước có 2 người, hai nước còn lại, mỗi nước 1 người là:.
Số cách chọn 4 người đủ các nước và toàn đại biểu nam là:
Số cách chọn 4 người đủ các nước và toàn đại biểu nữ là:
Số phần tử của A là n(A) = 2499- 12 - 550 = 1937
Xác suất của biến cố A: