Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Thời gian của một dao động chính là một chu kì của con lắc lò xo.
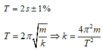
![]()
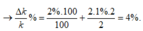

Chọn đáp án B
T = 2 π m k ⇒ k = 4 π 2 . m T 2
⇒ Δ k k = Δ m m + 2 Δ T T
= 2 % + 2.1 % = 4 %

Đáp án C
Phương pháp: Áp dụng công thức tính sai số trong thực hành thí nghiệm
Cách giải:
m = 100g ± 2%
T = 2s ± 2%
Ta có:
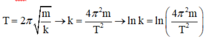
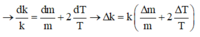
Ta có:
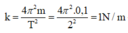
![]()

\(f=\frac{1}{2\pi}\sqrt{\frac{g}{\Delta l}}=\frac{1}{2\pi}\sqrt{\frac{\pi^2}{0.16}}=1.25Hz\)

Đáp án A
Sai số ngẫu nhiên các lần đo:
![]()
Sai số ngẫu nhiên trung bình sau n lần đo:
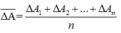
Sai số tuyệt đối
![]()
Sai số tỉ đối :

Sai số tỷ đối cho biết độ chính xác của phép đo.
Cách viết kết quả thực nghiệm :
![]()

Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)

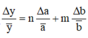
Chọn đáp án A
@ Lời giải:
+ Từ công thức xác định chu kì của con lắc lò xo