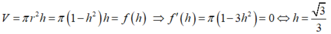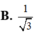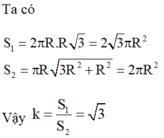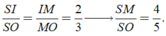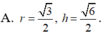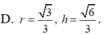Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
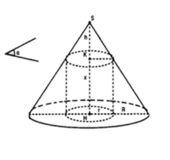
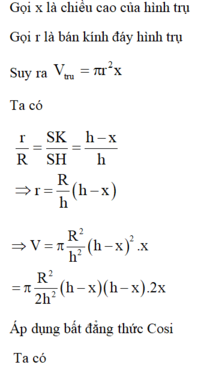
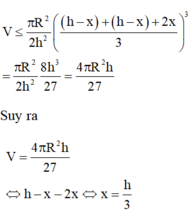
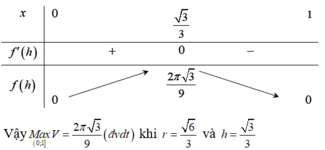
Vậy khi vị trí mặt phẳng α cách đáy hình nón một khoảng h 3 thì khối trụ có diện tích lớn nhất

Đáp án A.
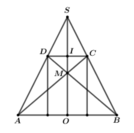
Gọi R là bán kính của hình cầu (S). Bài toán có thể quy về: “Cho đường tròn tâm O, bán kính R ngoại tiếp hình vuông ABCD và nội tiếp ∆ SEF đều” (hình vẽ).
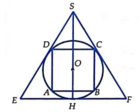
![]()
=>Bán kính đáy và chiều cao của hình trụ (T) lần lượt là
![]()
và ![]()
Thể tích khối trụ là
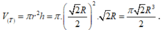
Ta có ∆ SEF đều và ngoại tiếp đường tròn (O) nên O là trọng tâm của ∆ SEF.
Gọi H là trung điểm của EF thì
Hình vuông ABCD nội tiếp đường tròn (O) nên SH = 3OH = 3R![]()
Bán kính đáy và chiều cao của hình nón (N) lần lượt là ![]()
Thể tích khối nón là
![]()
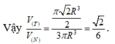

Đáp án B.
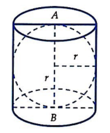
Gọi r là bán kính của mặt cầu nối tiếp
=> Diện tích xung quanh của mặt cầu là ![]()
![]()
=> Chiều cao của hình trụ là 4
=> Diện tích của hình trụ là ![]()

Chọn đáp án C
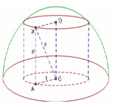
Hình trụ nội tiếp nửa mặt cầu, nên theo giả thiết đường tròn đáy trên có tâm O’ là hình chiếu của O xuống mặt đáy (O’). Suy ra hình trụ và nửa mặt cầu cùng chung trục đối xứng và tâm của đáy dưới hình trụ trùng với tâm O của nửa mặt cầu.
![]()
Thể tích khối trụ là