Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt tại trọng tâm của tam giác và có giá trị:
q0=\(\dfrac{-q}{\sqrt{3}}=\dfrac{-6\cdot10^{-7}}{\sqrt{3}}C.\)

Đáp án B
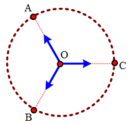
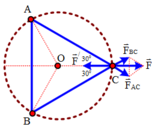
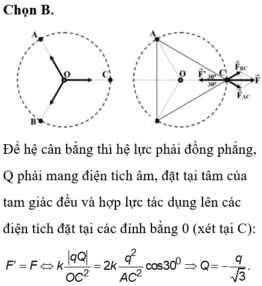
Để hệ cân bằng thì hệ lực phải đồng phẳng, Q phải mang điện tích âm, đặt tại tâm của tam giác đều và hợp lực tác dụng lên các điện tích đặt tại các đỉnh bằng 0 (xét tại C):
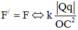
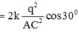
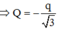

a.Vì q1 > 0 mà chúng đẩy nhau nên q2 > 0
F= \(\frac{k.\left|q_1q_2\right|}{r^2}\)
\(\Rightarrow\left|q_2\right|=\frac{F.r^2}{\left|q_1\right|}=\frac{6,75.10^{-5}.0,02^2}{\left|4.10^{-8}\right|}=0,675\left(C\right)\)
=>q2 =0,675 C
b)
b) \(E_{q_1}=\frac{k.\left|q_1\right|}{BH^2}=\frac{9.10^9.\left|4.10^{-8}\right|}{0,01^2}=3,6.10^6\frac{V}{m}\)
\(E_{q_2}=\frac{k.\left|q_2\right|}{AH^2}=\frac{9.10^9.\left|0,675\right|}{0,01^2}=6,075.10^{13}\frac{V}{m}\)
Vì vecto E1 ↑↑ vecto E2=>E=|E1-E2|=6,075.1013 V/m
\(E_{q_3}=\frac{k.\left|q_3\right|}{AH^2}=\frac{9.10^9.\left|-2.10^{-8}\right|}{\left(0,02.\sin45^o\right)^2}=621,5.10^3\frac{V}{m}\)
Vì vecto E vuông góc với Eq3 nên:
EH =\(\sqrt{E_{q_3}^2+E^2}=6,075.10^{13}\left(\frac{V}{m}\right)\)
Đáp án B
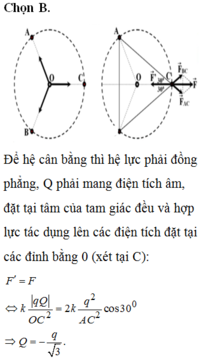
Để hệ cân bằng thì hệ lực phải đồng phẳng, Q phải mang điện tích âm, đặt tại tâm của tam giác đều và hợp lực tác dụng lên các điện tích đặt tại các đỉnh bằng 0 (xét tại C).
F ' = F ⇔ k Q q O C 2 = 2 k q 2 A C 2 cos 30 0 ⇒ Q = - q 3