Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Số cách lên toa của 7 người là: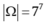 
Ta tìm số khả năng thuận lợi của A như sau
Chọn 3 toa có người lên: 
Với toa có 4 người lên ta có: 
cách chọn
Với toa có 2 người lên ta có: 
cách chọn
Người cuối cùng cho vào toa còn lại nên có 1 cách
Theo quy tắc nhân ta có: 
Do đó: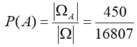 
.
Chọn A.
Đáp án B
Mỗi hành khách có 4 cách chọn 1 toa để lên tàu nên số cách 4 hành khách chọn toa để lên tàu là 
cách. Suy ra 
Gọi A là biến cố: “một toa có 3 hành khách; một toa có 1 hành khách và hai toa không có hành khách”.
Chon 3 hành khách từ 4 hành khách và xếp 3 hành khách vừa chọn lên 1 trong 4 toa tàu có 
cách
Xếp hành khách còn lại lên 1 trong 3 toa tàu còn lại có 3 cách
Suy ra 
Vậy xác suất của biến cố cần tìm là
Đáp án C.
Gọi 
là tập tất cả các dãy số 
trong đó 
là số toa mà hành khách thứ i lên 
+ 
là tập các cách lên tàu sao cho có 2 toa có 3 người và mỗi toa còn lại 1 người
+ 
là tập các cách lên tàu sao cho có 2 toa có 2 người và 1 toa có 1 người
là biến cố “Mỗi toa đều có hành khách lên tàu”
Chọn A
Số phần tử không gian mẫu: 
Gọi A là biến cố: Mỗi toa có ít nhất một khách lên tàu .
Có hai trường hợp:
TH1: Một toa có 3 khách 2 toa còn lại mỗi toa có 1 khách.
Trường hợp này có: 
(cách).
TH 2: Một toa có 1 khách 2 toa còn lại mỗi toa có 2 khách.
Trường hợp này có:
(cách).
Số kết quả thuận lợi của biến cố A là: n(A) = 150(cách).
Xác suất của biến cố A : 
Mỗi hành khách có 3 lựa chọn \(\Rightarrow n\left(\Omega\right)=3^{12}\)
Chọn 4 người lên toa 1: \(C_{12}^4\) cách
Còn lại 8 người lên 2 toa còn lại, có \(2^8\) cách
Xác suất: \(\dfrac{C_{12}^4.2^8}{3^{12}}=...\)
.
Đáp án B
Số cách để 4 vị khách lên tàu là: 
Số cách để chọn 3 vị khách lên một toa tàu là 
Số cách chọn 1 trong 3 toa là 
Vị khách còn lại có 2 cách chọn lên toa tàu
Vậy số cách để 1 trong 3 toa tàu chứa 3 trong 4 vị khách là: 3.4.2=24
\(cos\left(\frac{x}{2}+15^0\right)=sinx=cos\left(90^0-x\right)\)
\(\Rightarrow\left[{}\begin{matrix}\frac{x}{2}+15^0=90^0-x+k360^0\\\frac{x}{2}+15^0=x-90^0+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=50^0+k240^0\\x=210^0+k720^0\end{matrix}\right.\)
Với \(k=1\Rightarrow x=290^0\)
Bài 2:
\(\Leftrightarrow2sinx+2sinx.cosx-cosx-cos^2x-sin^2x=0\)
\(\Leftrightarrow2sinx+2sinx.cosx-cosx-1=0\)
\(\Leftrightarrow2sinx\left(cosx+1\right)-\left(cosx+1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(cosx+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=\frac{1}{2}\\cosx=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\) đáp án B
3/ \(y=\frac{sinx+cosx-1}{sinx-cosx+3}\)
\(\Leftrightarrow y.sinx-y.cosx+3y=sinx+cosx-1\)
\(\Leftrightarrow\left(y-1\right)sinx-\left(y+1\right)cosx=-3y-1\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(y-1\right)^2+\left(y+1\right)^2\ge\left(-3y-1\right)^2\)
\(\Leftrightarrow7y^2+6y-1\le0\)
\(\Rightarrow-1\le y\le\frac{1}{7}\Rightarrow y_{max}=\frac{1}{7}\)
a.
\(sinx+cosx+\left(sinx+cosx\right)^2+cos^2x-sin^2x=0\)
\(\Leftrightarrow sinx+cosx+\left(sinx+cosx\right)^2+\left(cosx-sinx\right)\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(1+2cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\\1+2cosx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\frac{\pi}{4}\right)=0\\cosx=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{4}+k\pi\\x=\pm\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
Mỗi một cách lên toa thỏa yêu cầu bài toán chính là một hoán vị của 7 phần từ nên ta có: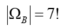
Do đó: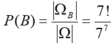
Chọn D.