Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. con người
2. bác tài bỏ lại xe đó và đi qua cầu
3. vì chúng bò theo đường thẳng nằm ngang
4.tôi sẽ bị treo cổ
5. đập con ma xanh trước, con ma đỏ thấy thế sợ quá mặt mày chuyển sang màu xanh, đập thêm phát nữa là chết cả 2 con.
6. con cua xanh vì cua đỏ đã được luộc chín rồi.

- Gọi số xe loại A và loại B cần dùng là x và y xe .
=> Số tiền là : \(T=4x+3y\)
Mà \(\left\{{}\begin{matrix}20x+10y\ge140\\0,6x+1,5y\ge9\end{matrix}\right.\) và \(\left\{{}\begin{matrix}x\ge0\\y\ge0\end{matrix}\right.\)
Ta có :

a) Gọi A là tập hợp học sinh giỏi, B là tập hợp học sinh được hạnh kiểm tốt của lớp 10A, thì A ∩ B là tập hợp các học sinh vừa giỏi, vừa có hạnh kiểm tốt.
Tập hợp học sinh được khen thưởng là A ∪ B. Số phân tử của A ∪ B bằng só phân tử của A cộng với số phân tử của B bớt đi số phân tử của A ∩ B (vì được tính hai lần).
– Vậy số học sinh lớp 10A được khen thưởng là:
15 + 20 – 10 = 25 người.
b) Số bạn lớp 10A chưa học giỏi và chưa có hạnh kiểm tốt là số học sinh lớp 10A chưa được khên thưởng bằng:
45 – 25 = 20 người.
a) Gọi A là tập hợp học sinh giỏi, B là tập hợp học sinh được hạnh kiểm tốt của lớp 10A, thì A ∩ B là tập hợp các học sinh vừa giỏi, vừa có hạnh kiểm tốt.
Tập hợp học sinh được khen thưởng là A ∪ B. Số phân tử của A ∪ B bằng só phân tử của A cộng với số phân tử của B bớt đi số phân tử của A ∩ B (vì được tính hai lần).
- Vậy số học sinh lớp 10A được khen thưởng là:
15 + 20 - 10 = 25 người.
b) Số bạn lớp 10A chưa học giỏi và chưa có hạnh kiểm tốt là số học sinh lớp 10A chưa được khên thưởng bằng:
45 - 25 = 20 người.

Chọn A
Gọi x; y lần lượt là số xe loại M, loại F cần thuê
Từ bài toán ta được hệ bất phương trình
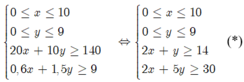
Tổng chi phí T(x; y) = 4x+ 3y (triệu đồng)
Bài toán trở thành là tìm x; y nguyên không âm thoả mãn hệ (*) sao cho T( ;xy) nhỏ nhất.
Từ đó ta cần thuê 5 xe hiệu M và 4 xe hiệu F thì chi phí vận tải là thấp nhất.

a) Điều kiện cần và đủ để một số chia hết cho 9 là tổng các chữ số của nó chia hết cho 9.
b) Điều kiện cần và đủ để tứ giác là hình thoi là tứ giác là hình bình hành có hai đường chéo vuông góc với nhau.
c) Điều kiện cần và đủ để phương trình bậc hai có hai nghiệm phân biệt là biệt thức của nó dương.
a) Điều kiện cần và đủ để một số chia hết cho 9 là tổng các chữ số của nó chia hết cho 9.
b) Điều kiện cần và đủ để tứ giác là hình thoi là tứ giác là hình bình hành có hai đường chéo vuông góc với nhau.
c) Điều kiện cần và đủ để phương trình bậc hai có hai nghiệm phân biệt là biệt thức của nó dương.

Gọi R là bán kính của đường tròn (C)
(C) và C1 tiếp xúc ngoài với nhau, cho ta:
MF1 = R1+ R (1)
(C) và C2 tiếp xúc ngoài với nhau, cho ta:
MF2 = R2 – R (2)
Từ (1) VÀ (2) ta được
MF1 + MF2 = R1+ R2= R không đổi

Điểm M có tổng các khoảng cách MF1 + MF2 đến hai điểm cố định F1 và F2 bằng một độ dài không đổi R1+ R2
Vậy tập hợp điểm M là đường elip, có các tiêu điểm F1 và F2 và có tiêu cự
F1 .F2 = R1+ R2
