Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là số nhà không có khách thuê thì giá thuê một căn nhà là 3 + 0,3x
Số tiền mà công ty thu được là M
M = 30 - x 3 + 0 , 3 x = - 0 , 3 x 2 + 6 x + 90 = - 0 , 3 x - 10 2 + 120 ⇒ M = 120
Vậy số tiên công ty có thể thu về lớn nhất là 120 triệu với giá cho thuê 6 triệu một căn.
Đáp án cần chọn là C

Giả sử giá thuê mỗi căn hộ là 2000000 + 10000 x (đồng/tháng). Khi đó, theo đề bài số căn hộ bị bỏ trống là 2x và số căn hộ được thuê là 50 - 2x. Do đó số tiền công ty thu được mỗi tháng là
S = 2000000 + 100000 x 50 - 2 x = 200000 20 + x 25 - x
Để công ty thu được nhiều lợi nhuận nhất, ta cần tìm x ∈ 0 ; 25 sao cho hàm số f(x) = ( 20 + x)( 25 - x ) đạt giá trị lớn nhất
Ta có f ' x = 5 - 2 x ; f ' x = 0 ⇔ x = 5 2
Lập bảng biến thiên ta thu được m a x x ∈ 0 ; 25 f x = 2025 4 = x = 5 2
Khi đó, giá thuê cho mỗi căn hộ là
2000000 + 100000 . 5 2 = 2250000 (đồng/tháng)
Đáp án A

Đáp án D
Gọi giá căn hộ là x(đồng) thì giá nhà tăng là x-2000000 từ đó số căn hộ được thuê là 50 − 2 x − 2000000 100000 Tư đó số tiền doanh thu là
S = x 50 − 2 x − 2000000 100000 = − 2 x 2 + 9000000 x 100000 = − 2 x − 2250000 2 100000 + 101250000
Vậy số tiên đạt giá trị lớn nhất khi x = 2250000.

Gọi x là số lần tăng 200 nghìn đồng (x > 0) để ông Bình thu được tổng số tiền nhiều nhất trên một tháng.
Khi đó ông Bình cho thuê được số phòng là: (20-x) phòng.
Tổng số tiền ông Bình thu được trên một tháng là:
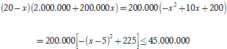
Dấu "=" xảy ra khi và khi x = 5.
Vậy ông Bình thu được tổng số tiền nhiều nhất trên một tháng khi ông tăng giá lên mức mỗi căn triệu đồng một tháng. Chọn C.

Đáp án B
Gọi x là số lần tăng tiền => Số tiền thuê một phòng là 1000000 + 50000x
Số phòng thuê được là 50 - x. Khi đó, số tiền thu được là


Đặt giá phòng là x. Thu nhập f(x)
bài toán được phát biểu lại dưới dạng thuần túy Toán học như sau:
Tìm x sao cho f(x) lớn nhất biết rằng khi x = 400 thì f(400) = 400x50, mỗi khi x tăng thêm 20 đơn vị thì f(x+20k) = (x+20k)x(50-2k).
Giá đã tăng: x - 400 (ngàn đồng).
Số phòng cho thuê giảm nếu giá là x:

Số phòng cho thuê với giá x là:

Trả lời câu 1: Thay giá trị x = 500 vào biểu thức trên ta được giá trị cần tìm là 40.
Doanh thu là: f(x) =

Trả lời câu 2: Thế f(x) = 20200 vào phương trình trên, giải phương trình bậc hai, ta được x = 427,64 hoặc x= 472,36
f’(x)=

f’’(x)= -1/5
f’(x) = 0, tương đương x = 450.
và f’’(450) = -1/5< 0
Trả lời câu 3: Theo trên thì x = 450 là cực đại và là cực trị duy nhất.
Tuấn Anh Phan Nguyễn
Đặt giá phòng là x. Thu nhập f(x)
Bài toán được phát biểu lại dưới dạng thuần túy toán học như sau:
Tìm x sao cho f(x) lớn nhất biết rằng khi x = 400 thì f(400) = 400x50, mỗi khi x tăng thêm 20 đơn vị thì f(x+20k) = (x+20k)x(50-2k).
Giá đã tăng: x - 400 (ngàn đồng).
Số phòng cho thuê giảm nếu giá là x:

Số phòng cho thuê với giá x là:

Trả lời câu 1: Thay giá trị x = 500 vào biểu thức trên ta được giá trị cần tìm là 40.
Doanh thu là: f(x) =

Trả lời câu 2: Thế f(x) = 20200 vào phương trình trên, giải phương trình bậc hai, ta được x = 427,64 hoặc x= 472,36
f’(x)=

f’’(x)= -1/5
f’(x) = 0, tương đương x = 450.
và f’’(450) = -1/5< 0
Trả lời câu 3: Theo trên thì x = 450 là cực đại và là cực trị duy nhất.

Chọn C.
Phương pháp: Đây là bài toán vay trả góp công thức để tính là
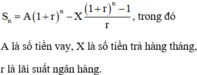
Cách giải: Theo công thức trên ta có phương trình:


Đáp án C