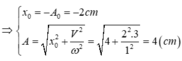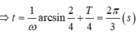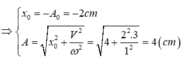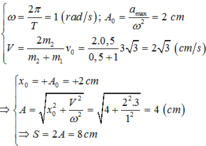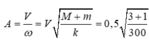Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những bài liên quan đến va chạm đàn hồi đã được giảm tải bạn nhé, chỉ quan tâm đến va chạm mềm thôi.
Bài này phải sửa lại khi lò xo có độ dài cực đại thì gia tốc là 2(cm/s^2)
- Khi vật m1 ở vị trí lò xo có độ dài cực đại ---> ở biên --> vận tốc = 0.
- \(\omega=\frac{2\pi}{T}=1\)(rad/s)
- Biên độ: \(A=\frac{a_{max}}{\omega^2}=\frac{2}{\left(1\right)^2}=2cm\)
- Xét sự va chạm giữa m2 và m1:
+ Bảo toàn động lượng: \(p_t=p_s\Leftrightarrow m_2v=m_1v_1+m_2v_2\Leftrightarrow m_2v=2m_2v_1+m_2v_2\Leftrightarrow v=2v_1+v_2\)(1)
+ Bảo toàn động năng: \(W_{đt}=W_{đs}\Leftrightarrow\frac{1}{2}m_2v^2=\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2\Leftrightarrow m_2v^2=2m_2v_1^2+m_2v_2^2\Leftrightarrow v^2=2v_1^2+v_2^2\)
\(\Leftrightarrow\left(v-v_2\right)\left(v+v_2\right)=2v_1^2\Leftrightarrow2v_1\left(v+v_2\right)=2v_1^2\Leftrightarrow v+v_2=v_1\)(2)
Từ (1) và (2) suy ra: \(v_1=\frac{2}{3}v=\frac{2}{3}3\sqrt{3}=2\sqrt{3}\)(cm/s)
\(v_2=v_1-v=2\sqrt{3}-3\sqrt{3}=-\sqrt{3}\)(cm/s) (dấu - là do vật 2 chuyển động ngược lại)
- Sau va chạm, vật m1 có li độ 2cm, vận tốc: \(2\sqrt{3}cm\)
--> Biên độ dao động mới là: \(A'=\sqrt{x^2+\left(\frac{v}{\omega}\right)^2}=\sqrt{2^2+\left(\frac{2\sqrt{3}}{1}\right)^2}=4cm\)
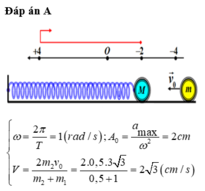
+ Thời gian kể từ sau va chạm đến khi vật m1 đổi chiều chuyển động (ở biên) là: \(\Delta t=\frac{150}{360}T=\frac{120}{360}.2\pi=\frac{2}{3}\pi\)(s)
+ Quãng đường vật m2 đi được trong thời gian này là: \(S=v.\Delta t=\sqrt{3}.\frac{2}{3}\pi\simeq3,63cm\)
Khoảng cách giữa 2 vật: \(4+2+3,63=9,63\)(cm)
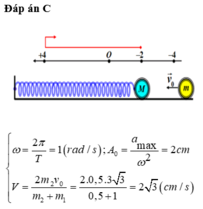
Đáp án C

Giải thích: Đáp án D
Phương pháp :
- Áp dụng định luật bảo toàn động lượng và định luật bảo toàn động năng
- Sử dung̣ hê ̣thức đôc̣ lâp̣ với thời gian của li đô ̣vàvâṇ tốc
Biên độ dao động ban đầu: ![]()
Cách giải:
Hai vật va chạm đàn hồi xuyên tâm nên áp dụng ĐL bảo toàn động lượng và động năng ta được:
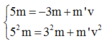
Giải hệ ta được v = 2cm/s
Áp dụng hệ thức độ lập: 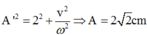
Vậy quãng đường đi được sau va chạm đến khi đổi chiều chuyển động là

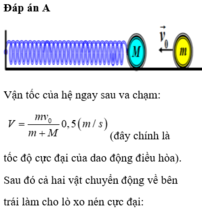
Hướng dẫn: Chọn đáp án A
Vì va chạm mềm nên tốc độ của hai vật ngay sau va chạm:
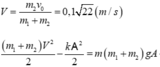
![]()

![]()
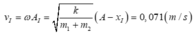

Đáp án B
Phương pháp: Áp dụng định luật bảo toàn động lượng và lí thuyết về bài toán thay đổi tần số góc trong dao động điều hòa
Cách giải:
- Áp dụng định luật bảo toàn động lượng cho vật M và m trước và sau khi va chạm ta có:
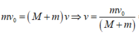
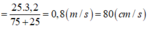
- Sau khi va chạm, con lắc lò xo sẽ dao động điều hòa với tần số góc
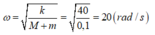
- Vận tốc khi đi qua vị trí cân bằng là vận tốc cực đại:
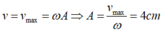

Va chạm mềm, động lượng được bảo toàn.
Động lượng trước: \(p_t=0,25.4=1(kgm/s)\)
Động lượng sau: \(p_s=(0,25+0,15).v=0,4.v\)
\(p_t=p_s\Rightarrow 0,4.v=1\Rightarrow v=2,5(m/s)\)
Cơ năng của hệ chính là động năng sau va chạm: \(W=\dfrac{1}{2}.0,4.2,5^2=1,25(J)\)