Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A là biên độ giao động ta có : kA = 10 N; kA2/2 = 1J => A = 0,2 m = 20 cm
Khoảng thời gian ngắn nhất giữa 2 lần liên tiếp Q chịu tác dụng lực kéo của lò xo có độ lớn \(5\sqrt{3}\)
=> Chu kì giao động của vật T = 0,6s
Quãng đường ngắn nhất đi được là trong 0,4s = \(\frac{2T}{3}\) là s = 3A = 60 cm
Vậy B đúng

Ta có: 1/2 k.A^2=0,32
k.A=8
=>A=0,08m
lực kéo của lò xo có độ lớn 4.căn 3=(8.căn 3)/2. Dùng đường tròn lượng giác => góc quét là pi/3 =>t=T/6=0,2=>T=1,2
Quãng đường lớn nhất đi đc trong 0,8s=2T/3=T/2+T/6
Quãng đường đi đc trong T/2 là 2A
Quãng đường đi đc trong T/6 ứng vs góc quét pi/3 đi từ A/2 đến -A/2 =>Quãng đường là A=0,08m = 80 cm
3 dòng đầu tiên ý...giải thích giúp mình đc k???đề bài cho là 1J mà...mới cả k đã biết đâu nữa???

Khoảng thời gian ngắn nhất giữa hai lần liên tiếp vật vật đi qua vị trí có li độ
![]()
+ Lực kéo cực đại của lò xo tác dụng và điểm có định là
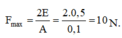
+ Vậy khoảng thời gian ngắn nhất để lò xo kéo điểm cố định một lực 5 N là
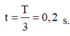
Đáp án D

Fmax=kA=10N
W=12kA2=1J
→A=20cm
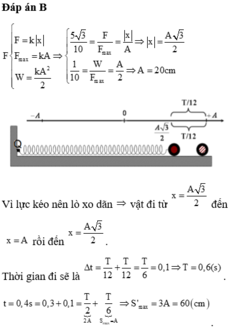
Vẽ trục thời gian đối với lực đàn hồi, biên độ là A = 10N. Tìm được thời gian ngắn nhất là \(\frac{T}{6}\) (vị trí lực kéo bằng 5√3N chính là vị trí \(\frac{A\sqrt{3}}{2}\))
Tính T
Tìm tỉ số \(\frac{\Delta t}{T}=\frac{0,4}{0,6}=\frac{2}{3}\)
\(\rightarrow\Delta t=\frac{T}{2}+\frac{T}{6}\)
\(S_{max}\)\(=2A+A=3A=60cm\)

\(F=\frac{F_{max}\sqrt{3}}{2}\rightarrow t_{min}=\frac{T}{6}=0,1s\rightarrow T=0,6s\)
Từ biểu thức tính năng lượng, tìm được A = 20cm
\(\Delta t=0,4s=\frac{T}{2}+\frac{T}{6}\)
\(\rightarrow S_{max}=2A+A\)
\(S_{max}=60cm\)
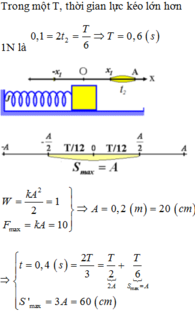
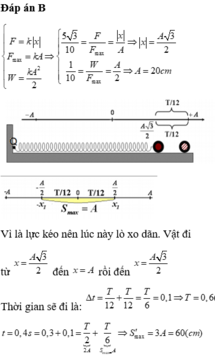

Chọn C.
Khoảng thời gian ngắn nhất ứng với quay được góc nhỏ nhất