Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tần số dao động: \(f=\frac{\omega}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{36}{0,1}}=3Hz\)
Trong dao động điều hòa, động năng và thế năng biến thiên với tần số gấp đôi tần số dao động.
\(\Rightarrow f'=2.3=6Hz\)

Đáp án A
+ Tần số góc của dao động f = 1 2 π k m = 3 Hz, vậy động năng của con lắc sẽ biến thiên với tần số 6 Hz

\(x=A\cos\left(\omega t+\varphi\right)\Rightarrow x'=v=\omega A\sin\left(\omega t+\varphi\right)\)
\(W_d=\dfrac{1}{2}mv^2=\dfrac{1}{2}.m.\omega^2A^2\sin^2\left(\omega t+\varphi\right)\)
\(=\dfrac{1}{2}kA^2.\dfrac{1}{2}\left[1-\cos2\left(\omega t+\varphi\right)\right]\)
\(=\dfrac{1}{4}kA^2\left[1-\cos\left(2\omega t+2\varphi\right)\right]\)
\(\Rightarrow f_{W_d}=2f_x=2.\dfrac{\omega}{2\pi}=\sqrt{\dfrac{k}{m.\pi^2}}=10\left(Hz\right)\)

Đáp án D
Phương pháp: Động năng của con lắc biến thiên tuần hoàn theo thời gian với tần số bằng hai lần tần số của vật dao động điều hoà
Cách giải :
Động năng của con lắc biến thiên tuần hoàn theo thời gian với tần số
f = 2 . 1 2 π = k m = 6 Hz

Đáp án A
Phương pháp: Động năng của con lắc biến thiên theo thời gian với tần số bằng 2 lần tần số của dao động điều hoà
Cách giải:
Gọi f là tần số dao động của con lắc thì động năng của con lắc biến thiên theo thời gian với tần số 2f
Tần số dao động: f = 1 2 π k m = 1 2 π 36 0 , 1 = 3 Hz
Vậy động năng của con lắc biến thiên theo thời gian với tần số f’ = 2.3 = 6Hz

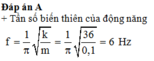
Đáp án C