Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
+Khi có lực lạ gia tốc trọng trường biểu kiến 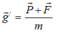
Trong trường hợp cụ thể:
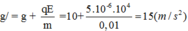
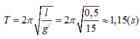


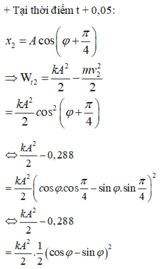


Thời gian lò xo giãn trong một chu kì được biểu diễn trên đường tròn lượng giác:

Đáp án D

Bạn áp dụng CT của dao động điều hòa:
\(A^2=x^2+\dfrac{v^2}{\omega^2}\)
Với \(x=\alpha.\ell\), li độ là độ dài cung của góc \(\alpha\) (tính theo rad)
\(\Rightarrow (\alpha_0.\ell)^2=(\alpha.\ell)^2+\dfrac{v^2.\ell}{g}\)
\(\Rightarrow \alpha_0^2=\alpha^2+\dfrac{v^2}{g\ell}\)
Chọn đáp án A.

Đáp án C
Phương pháp:
Công thức tính chu kì: 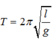
Sử dụng công thức tính sai số trong thực hành thí nghiệm
Cách giải: Ta có: 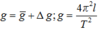
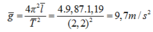

![]()

Đáp án D
Phương pháp: Thế năng đàn hồi : Thế năng đàn hồi :
Cách giải:
Độ dãn của lò xo tại vị trí cân bằng: ![]()
Biên độ dao động của con lắc: A = 7,5 - Δl0 = 7,5 - 2,5 = 5cm
Ta có: Δl0< A
Chọn chiều dương hướng xuống
=> Vị trí lực đàn hồi có độ lớn nhỏ nhất là vị trí lò xo hông giãn cũng hông nén: Δl = 0
Thế năng đàn hồi tại vị trí đó: 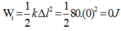
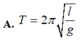
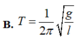
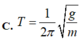


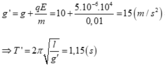
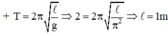
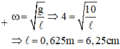
Chu kì dao động của con lắc đơn
Đáp án A