Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kiến thức áp dụng
+ Diện tích hình tròn bán kính R là: S = πR2.

Theo các buộc thứ nhất thì diện tích cỏ dành cho mỗi con dê là bằng nhau.
Mỗi diện tích là 1/4 hình tròn bán kính 20m.
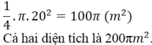 (1)
(1)
Theo cách thuộc thứ hai, thì diện tích cỏ dành cho con dê buộc A là:

So sánh (1) và (2) ta thấy với cách buộc thứ 2 thì diện tích cỏ mà hai con dê có thể ăn được sẽ lớn hơn

Theo cách buộc thứ nhất thì diện tích cỏ dành cho mỗi con dê là bằng nhau.
Mỗi diện tích là hình tròn bán kính 20m.
π.202 = 100π (m2)
Cả hai diện tích là 200π (m2) (1)
Theo cách buộc thứ hai, thì diện tích cỏ dành cho con dê buộc ở A là
π.302 =
900π (m2)
Diện tích cỏ dành cho con dê buộc ở B là: π.102 =
100π (m2)
Diện tích cỏ dành cho cả hai con dê là:
900π +
100π =
1000π = 250π (m2) (2)
So sánh (1) và (2) ta thấy với cách buộc thứ hai thì diện tích cỏ mà hai con dê có thể ăn được sẽ lớn hơn.
Theo cách buộc thứ nhất thì diện tích cỏ dành cho mỗi con dê là bằng nhau. Mỗi diện tích là 1/4 hình tròn bán kính 20m. 1/4.π.202 = 100π (m2) Cả hai diện tích là 200π (m2) (1) Theo cách buộc thứ hai, thì diện tích cỏ dành cho con dê buộc ở A là 1/4 π.302 = 1/4 900π (m2) Diện tích cỏ dành cho con dê buộc ở B là: 1/4 π.102 = 1/4. 100π (m2) Diện tích cỏ dành cho cả hai con dê là:1/4.900π + 1/4.100π = 1/4.1000π = 250π (m2) (2) So sánh (1) và (2) ta thấy với cách buộc thứ hai thì diện tích cỏ mà hai con dê có thể ăn được sẽ lớn hơn.

Gọi số con trâu và bò lần lượt là $x,y(x,y>0)$
$\to x+y=30(1)$
Một tuần mỗi con trâu ăn hết 5 bó cỏ có, mỗi con bò ăn hết 3 bó cỏ mà cps 120 bó cỏ nên ta có phương trình:
$5x+3y=120(2)$
Từ (1) và (2) ta có HPT:
$\begin{cases}x+y=30\\5x+3y=120\\\end{cases}$
$\to \begin{cases}3x+3y=90\\5x+3y=120\\\end{cases}$
$\to \begin{cases}2x=30\\x+y=30\\\end{cases}$
$\to \begin{cases}x=15\\y=15\\\end{cases}$
Vậy có 15 con trâu.


