Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc nước chảy là vn (km/h)
Ta có: \(\left\{{}\begin{matrix}AB=\left(v_n+v\right)t\\AB=\left(v-v_n\right)t\end{matrix}\right.\)\(\Rightarrow\left(30+v_n\right)2=\left(30-v_n\right)3\)
\(\Rightarrow v_n=6\) km/h
Khoảng cách AB là: \(AB=\left(v_n+v\right)t=\left(30+6\right)2=72km\)
Câu B

Chọn D
+ Gọi v 13 là vận tốc của thuyền với bờ
v 23 là vận tốc của nước với bờ bằng
v 12 là vận tốc của thuyền so với dòng nước
+ Khi xuôi dòng: v 13 = v 12 + v 23
+ Khi ngược dòng: v 13 = v 12 - v 23 ⇒ v 13 - v 13 = 2 v 23
⇔ S 2 , 5 - S 3 = 2 . v 23 ⇒ v 23 = 1 2 ( S 2 , 5 - S 3 ) ⇒ t c = S v 23 = 30 h

Giải: Gọi v 13 là vận tốc của xuồng với bờ; v 23 là vận tốc của nước với bờ bằng 4 km/h; v 12 là vận tốc của xuồng so với dòng nước
Ta có: Khi đi xuôi dòng: v 13 = v 12 + v 23
Mà S A B = v 13 . t 1 = ( v 12 + v 23 ) . 4
Khi đi ngược dòng: v 13 = v 12 – v 23
Mà S A B = v 13 . t 2 = ( v 12 – v 23 ) . 5
Quãng đường không đổi: v 12 + v 23 . 4 = v 12 – v 2 3 . 5 ⇒ v 12 = 36 k m / h ⇒ S A B = 160 k m

Chọn A
+ Gọi v 13 là vận tốc của xuồng với bờ
v 23 là vận tốc của nước với bờ bằng 4 km/h
v 13 là vận tốc của xuồng so với dòng nước
Khi đi xuôi dòng:
![]()
+ Mà ![]()
+ Khi đi ngược dòng: ![]()
+ Mà ![]()
+ Quãng đường không đổi: ![]()
![]()

\(2\left(\dfrac{m}{s}\right)=7,2\left(\dfrac{km}{h}\right)\)
Ta có:
+ Thời gian xuôi dòng:
\(t_{xd}=\dfrac{AB}{v_{tn}+v_{nb}}=1\Rightarrow AB=v_{tn}+v_{nb}\left(1\right)\)
+ Thời gian ngược dòng:
\(t_{nd}=\dfrac{AB}{v_{tn}-v_{nb}}=3\Rightarrow AB=3v_{tn}-3v_{nb}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow v_{tn}=14,4\left(\dfrac{km}{h}\right)=4\left(\dfrac{m}{s}\right)\)


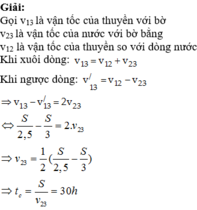

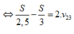


Đáp án B