Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

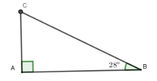
Ta có độ dài của mặt cầu trượt là AB, AC = 2,1m và A B C ^ = 28 0
Xét tam giác ACB vuông tại A có:
BC = AB : sin B = 2,1 : sin 28 0 ≈ 4,47m
Vậy độ dài của mặt cầu trượt là 4,47m
Đáp án cần chọn là: D

A B C 2,1
Biểu diễn các số đo như hình vẽ, ta có:
\(AB=\dfrac{2,1}{0,28}=7,5\left(m\right)\)
\(\Rightarrow AC=\sqrt{AB^2+BC^2}=\sqrt{7,5^2+2,1^2}\simeq7,8\left(m\right)\)

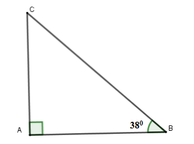
Ta có chiều cao cột đèn là AC; AB = 6m và A C B ^ = 38 0
Xét tam giác ACB vuông tại A có:
AC = AB. tan B = 6. tan 28 0 ≈ 4,68m
Vậy cột đèn cao 4,69m
Đáp án cần chọn là: B

a) Khoảng cách giữa 2 vị trí đó là :
\(\frac{20000}{180}.\left(72-42\right)\simeq2800\left(km\right)\)
b) Bán kính của Trái Đất là :
\(\frac{20000}{3,14}\simeq6400\left(km\right)\)
Độ dài đường xích đạo là :
\(20000.2=40000\left(km\right)\)
Vì trái đất là hình cầu :
Thể tích hình cầu được tính dưới dạng : \(V=\frac{4}{3}.3,14.R^3\)( R là bán kính )
Vậy thể tích Trái Đất là :
\(\frac{4}{3}.3,14.\left(6400\right)^3\simeq1097509547000\left(km^3\right)\)

Phương trình hoành độ giao điểm của (P) và (d) là \(x^2=mx-m+1\)\(\Leftrightarrow x^2-mx+m-1=0\)
Để (d) cắt (P) tại 2 điểm phân biệt thì \(\Delta=\left(-m\right)^2-4.1\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2>0\)\(\Leftrightarrow m-2\ne0\)\(\Leftrightarrow m\ne2\)
Khi đó \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=m-1\end{cases}}\)(hệ thức Vi-ét)
Độ dài cạnh huyền của tam giác vuông có 2 cgv là \(x_1,x_2\)là \(\sqrt{x_1^2+x_2^2}=\sqrt{\left(x_1+x_2\right)^2-2x_1x_2}=\sqrt{m^2-2\left(m-1\right)}=\sqrt{m^2-2m+2}\)
Ta có \(x_1x_2=\frac{1}{\sqrt{5}}\sqrt{m^2-2m+2}\)hệ thức lượng trong tam giác vuông.
\(\Leftrightarrow m-1=\frac{1}{\sqrt{5}}\sqrt{m^2-2m+2}\)\(\Leftrightarrow\frac{m-1}{\sqrt{m^2-2m+2}}=\frac{1}{\sqrt{5}}\)\(\Leftrightarrow\sqrt{\frac{m^2-2m+1}{m^2-2m+2}}=\sqrt{\frac{1}{5}}\)\(\Leftrightarrow\frac{m^2-2m+1}{m^2-2m+2}=\frac{1}{5}\)\(\Leftrightarrow5m^2-10m+5=m^2-2m+2\)\(\Leftrightarrow4m^2-8m+3=0\)
\(\Delta_1=\left(-8\right)^2-4.4.3=16>0\)
\(\Rightarrow\orbr{\begin{cases}m_1=\frac{-\left(-8\right)+\sqrt{16}}{2.4}=\frac{3}{2}\\m_2=\frac{-\left(-8\right)-\sqrt{16}}{2.4}=\frac{1}{2}\end{cases}}\)
Vậy để [...] thì \(\orbr{\begin{cases}m=\frac{3}{2}\\m=\frac{1}{2}\end{cases}}\)
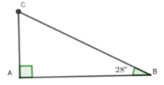

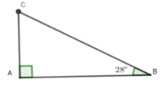

Ta có độ dài của mặt cầu trượt là AB, AC = 2,4m và A B C ^ = 25 0
Xét tam giác ACB vuông tại A có:
BC = AB : sin B = 2,4 : sin 25 0 ≈ 5,68m
Vậy độ dài của mặt cầu trượt là 5,68m
Đáp án cần chọn là: C