Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích phần giấy cứng cần tính chính là diện tích xung quanh của một hình hộp có đáy là hình vuông cạnh 4cm, chiều cao 1,2m = 120cm.
Diện tích xung quanh của hình hộp chính là diện tích bốn hình chữ nhật bằng nhau với chiều dài là 120 cm và chiều rộng 4cm::
S Xq = 4 . 4 . 120 = 1920 cm 2
Kiến thức áp dụng
Diện tích xung quanh của hình hộp chữ nhật: Sxq = 2(a + b).h
với a, b là độ dài hai cạnh của hình chữ nhật, h là chiều cao của hình chữ nhật.

* Diện tích phần giấy cứng dùng để làm một hộp:
Diện tích phần giấy cứng dùng để làm một hộp chính là diện tích xung quanh của hình hộp (vì hình hộp hở hai đầu và không tính lề và mép dán) và hình hộp này có đáy là một hình vuông cạnh là a (cm)
⇒ Sxq = 4a.h (1)
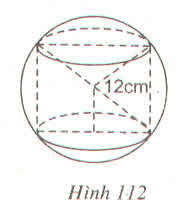
Từ hình vẽ ta thấy đáy của hình hợp là hình vuông ngoại tiếp đường tròn đường kính 4cm là đáy của bóng đèn. Suy ra a = 4cm (hình 112) và chiều dài của bóng đèn là chiều cao của hình hộp. Suy ra h = 1,2m = 120 cm
(1) ⇒ Sxq = 4.4.120 = 1920 (cm2)
Vậy diện tích phần giấy cứng dùng để làm một hộp là 1920 cm2

Áp dụng BĐT sau:\(2\left(a^2+b^2\right)\ge\left(a+b\right)^2\) ( dùng BĐT Bunhiacopski mà chứng minh :D )
Ta có:\(\frac{a+b}{a^2+b^2}=\frac{41}{9}\Rightarrow\frac{a^2+b^2}{a+b}=\frac{41}{9}\)
\(\Rightarrow\frac{82}{9}=\frac{2\left(a^2+b^2\right)}{a+b}\ge\frac{\left(a+b\right)^2}{a+b}=a+b\)
\(\Rightarrow a+b\le9\)
Mặt khác:\(41\left(a+b\right)=9\left(a^2+b^2\right);\left(41;9\right)=1\Rightarrow a+b⋮9\Rightarrow a+b=9\)
\(\Rightarrow a^2+b^2=41\)
Ta có hệ:\(\hept{\begin{cases}a+b=9\\a^2+b^2=41\end{cases}}\) giải cái hệ này là ra a,b nha < 3

Diện tích toàn phần một hộp:
4 . 1,2 . 0,02 = 0,096 (m²)
Diện tích giấy dùng để làm hộp bảo vệ cho 20 đèn:
20 . 0,096 = 1,92 (m²)

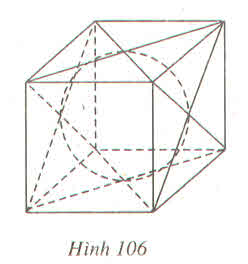
Ta thấy ngay cạnh của hình lập phương gấp đôi bán kính hình cầu
a) Tỉ số cần tính \(\dfrac{6}{\pi}\)
b) Diện tích toàn phần của hình lập phương là \(42cm^2\)
c) Thể tích cần tính xấp xỉ \(244cm^3\)

Từ các công thức tính thể tích hình cầu và hình trụ có thể suy ra kết quả là \(\dfrac{2}{3}\)
Vậy chọn (D)

a) Diện tích xung quanh của hình trụ : \(288\pi\left(cm^2\right)\)
b) Thể tích hình cầu : \(2304\pi\left(cm^3\right)\)
c) Diện tích mặt cầu : \(576\pi\left(cm^2\right)\)

:v Làm bài 31 thôi nhá , còn lại all tự làm -..-
Gọi x (cm) , y (cm) là độ dài hai cạnh góc vuông của tam giác vuông (x > 2, y > 4).
Diện tích tam giác ban đầu là \(\frac{1}{2}xy\left(cm^2\right)\)
+ Tăng mỗi cạnh lên 3cm thì tam giác vuông mới có độ dài 2 cạnh là x + 3(cm) và y + 3 (cm)
Diện tích tam giác mới là : \(\frac{1}{2}\left(x+3\right)\left(y+3\right)\left(cm^2\right)\)
Diện tích tăng thêm 36 cm2 nên ta có p/trình :
\(\frac{1}{2}\left(x+3\right)\left(y+3\right)=\frac{1}{2}xy+36\)
\(\Leftrightarrow\left(x+3\right)\left(y+3\right)=xy+72\)
\(\Leftrightarrow xy+3x+3y+9=xy+72\)
\(\Leftrightarrow3x+3y=63\)
\(\Leftrightarrow x+y=21\)
+ Giảm một cạnh 2cm và giảm cạnh kia 4cm thì tam giác vuông mới có 2 cạnh là : x – 2 (cm) và y – 4 (cm).
Diện tích tam giác mới là : \(\frac{1}{2}\left(x-2\right)\left(y-4\right)\left(cm^2\right)\)
Diện tích giảm đi 26cm2 nên ta có phương trình :
\(\frac{1}{2}\left(x-2\right)\left(y-4\right)=\frac{1}{2}xy-26\)
\(\Leftrightarrow\left(x-2\right)\left(y-4\right)=xy-52\)
\(\Leftrightarrow xy-4x-2y+8=xy-52\)
\(\Leftrightarrow4x+2y=60\)
\(\Leftrightarrow2x+y=30\)
Ta có hệ phương trình : \(\hept{\begin{cases}x+y=21\\2x+y=30\end{cases}}\)
Lấy phương trình thứ hai trừ phương trình thứ nhất ta được :
\(\hept{\begin{cases}\left(2x+y\right)-\left(x+y\right)=30-21\\x+y=21\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x+y-\left(x+y\right)=9\\x+y=21\end{cases}\Leftrightarrow\hept{\begin{cases}x=9\\y=12\end{cases}}}\)
Vậy tam giác có hai cạnh lần lượt là 9cm và 12cm




Diện tích phần giấy cứng cần tính chính là diện tích xung quanh của một hình hộp có đáy là hình vuông cạnh 4cm, chiều cao 1,2m = 120cm.
Diện tích xung quanh của hình hộp chính là diện tích bốn hình chữ nhật bằng nhau với chiều dài là 120 cm và chiều rộng 4cm::
Sxq= 4.4.120 = 1920 cm2