Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có:
Có 5 cách chọn hoa hồng trắng.
Có 6 cách chọn hoa hồng đỏ.
Có 7 cách chọn hoa hồng vàng.
Vậy theo qui tắc nhân ta có 5.6.7 = 210 cách.
Chọn đáp án B.

Đáp án : A
Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có:
Có 7 cách chọn hoa hồng trắng.
Có 5 cách chọn hoa hồng đỏ.
Có 6 cách chọn hoa hồng vàng.
Vậy theo qui tắc nhân ta có 7.5.6=210 cách.

Không gian mẫu là số cách chọn ngẫu nhiên 7 hoa từ ba bó hoa gồm 21 hoa.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố “7 hoa được chọn có số hoa hồng bằng số hoa ly”. Ta có các trường hợp thuận lợi cho biến cố A là:
● Trường hợp 1. Chọn 1 hoa hồng, 1 hoa ly và 5 hoa huệ nên có ![]() cách.
cách.
● Trường hợp 2. Chọn 2 hoa hồng, 2 hoa ly và 3 hoa huệ nên có ![]() cách.
cách.
● Trường hợp 3. Chọn 3 hoa hồng, 3 hoa ly và 1 hoa huệ nên có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là ![]() .
.
Vậy xác suất cần tính 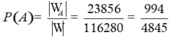
Chọn D.

Số cách chọn 2 bông bất kì: \(C_{18}^2\)
Số cách chọn 2 bông cùng màu: \(C_5^2+C_6^2+C_7^2\)
Số cách thỏa mãn: \(C_{18}^2-\left(C_5^2+C_6^2+C_7^2\right)=...\)

Chọn ngẫu nhiên 7 bông hoa tứ 3 bó ta có \(C^7_{21}\) cách.
Chọn 7 bông hoa trong đó số bông hoa hồng bằng số bông hoa ly xảy ra các trường hợp sau :
- Trường hợp 1 : Chọn 7 bông hoa trong đó có 1 bông hoa hồng, 1 bông hoa ly và 5 bông hoa huệ có \(C^1_8C^1_7C^5_6\) cách.
- Trường hợp 2 : Chọn 7 bông hoa trong đó có 2 bông hoa hồng, 2 bông hoa ly và 3 bông hoa huệ có \(C^2_8C^2_7C^3_6\) cách.
- Trường hợp 3 : Chọn 7 bông hoa trong đó có 3 bông hoa hồng, 3 bông hoa ly và 1 bông hoa huệ có \(C^3_8C^3_7C^1_6\) cách.
Từ các trường hợp trên ta có \(C^1_8C^1_7C^5_6+C^2_8C^2_7C^3_6+C^3_8C^3_7C^1_6=12306\) cách chọn 7 bông hoa trong đó số bông hoa hồng bằng số bông hoa ly.
Xác suất cần tính là : \(p=\frac{2015}{19380}\approx0.106\)

Không gian mẫu: \(C_{16}^3\)
a. Số cách chọn 3 bông cùng loại: \(C_5^3+C_7^3+C_4^3=...\)
Xác suất: \(P=\dfrac{C_5^3+C_7^3+C_4^3}{C_{16}^3}=...\)
b. Số cách chọn không có bông nhung nào: \(C_{11}^3\)
Số cách chọn có ít nhất 1 bông nhung: \(C_{16}^3-C_{11}^3\)
Xác suát: \(P=\dfrac{C_{16}^3-C_{11}^3}{C_{16}^3}\)


Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có:
Có 5 cách chọn hoa hồng trắng.
Có 6 cách chọn hoa hồng đỏ.
Có 7 cách chọn hoa hồng vàng.
Vậy theo qui tắc nhân ta có 5.6.7= 210 cách.
Chọn đáp án B.