Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : ADCT : \(I_0=U_0\sqrt{\frac{C}{L}}\) ( Từ công thức tính năng lượng điện từ trong mạch \(W=W_{Cmax}=W_{Lmax}\)
Nghĩa là :\(\frac{L.\left(I_0\right)^2}{2}=\frac{C.\left(U_0\right)^2}{2}\))
\(\Rightarrow I_0=5.\sqrt{\frac{8.10^{-9}}{2.10^{-4}}}=\text{0.0316227766}\left(A\right)\)\(\Rightarrow I=\frac{I_0}{\sqrt{2}}=\text{0.022360677977}\left(A\right)\)
Mà \(P=r.I^2\Rightarrow r=\frac{6.10^{-3}}{5.10^{-4}}=12\left(\Omega\right)\Rightarrow D\)

Đáp án D
+ Dòng điện cực đại trong mạch
I 0 = C L U 0 = 0 , 2 . 10 - 6 2 . 10 - 3 12 = 0 , 12 A
Công suất cung cấp cho mạch bằng công suất tỏa nhiệt trên điện trở
P = 0 , 5 I 0 2 R = 0 , 5 . 0 , 12 2 . 0 , 01 = 72 . 10 - 6 W

Đáp án A
+ Cường độ dòng điện cực đại trong mạch
1 2 C U 0 2 = 1 2 L I 0 2 ⇒ I 0 = C L U 0 = 3000 . 10 - 9 30 . 10 - 6 6 = 0 , 6 A .
Năng lượng cần cung cấp để duy trì dao động của mạch phải có công suất bằng công suất tỏa nhiệt trên điện trở
P = I 2 R = I 0 2 2 R = 0 , 6 2 2 1 = 0 , 18 W .

Đáp án C
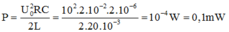
Lại có T = 2 π LC nên năng lượng cung cấp cho mạch trong một chu kỳ là:
![]()
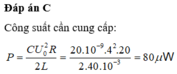

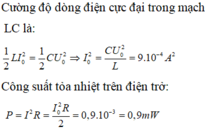
Đáp án B