Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Công suất cần cung cấp: ![]() (1)
(1)
Có: 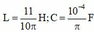
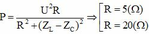
Thay vào (1) tìm được 

Đáp án C
+ Công suất tiêu thụ của mạch
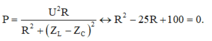
Phương trình trên cho ta hai nghiệm R = 20 Ω v à R = 50 Ω
+ Với mạch LC, ta có

=> Công suất tiêu hao lớn nhất ứng với
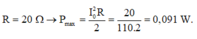

Giải thích: Đáp án C
Khi 3 phần tử mắc vào điện áp xoay chiều:
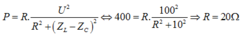
*Khi mắc 3 phần tử này cho mạch cùng dao động thì do năng lượng tiêu tốn là do điện trở, do đó ta cần cung cấp một công suất lớn nhất tương ứng là Pcc
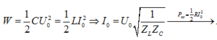
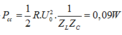
Chú ý: 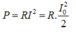

- Công suất tiêu thụ của mạch:
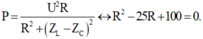
→ Phương trình trên cho ta hai nghiệm:
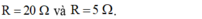
- Với mạch LC, ta có:
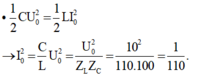
→ Công suất tiêu hao lớn nhất ứng với:
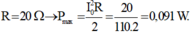

Giải thích: Đáp án C
Ta có: 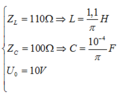
Công suất tiêu thụ của mạch:
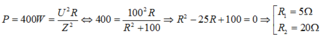
Công suất cung cấp cho mạch để duy trì dao động:
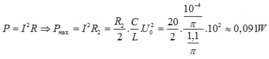

Khi dung kháng là $100 \Omega$ thì công suất tiêu thụ của đoạn mạch là cực đại bằng 100 W nên
\(\begin{cases} Z_L=Z_{C_1}=100 \Omega \\ P=\dfrac{U^2}{R} =100 W \end{cases}\)
Khi dung kháng là $200 \Omega$ thì điện áp hiệu dụng giữa hai đầu tụ điện là $100\sqrt{2} V$ nên
$U_{C_2}=\dfrac{U.Z_{C_2}}{Z}=\dfrac{200.U}{\sqrt{R^2+(100-200)^2}}=100\sqrt{2}$
$\Rightarrow 2U^2=R^2+100^2$
$\Rightarrow 2.100.R =R^2 +100^2$
$\Rightarrow R=100 \Omega$

Vì có điện trở thuần nên dao động trong mạch tắt dần do tỏa nhiệt ở điện trở. Để duy trì dao động điều hòa phải bổ sung cho mạch một năng lượng có công suất đủ bì vào phần năng lượng hao phí do tỏa nhiệt (hiệu ứng J un) trên điện trở, phần này có công suất là: \(\Delta P=I^2.R\)
Khi cùng cấp năng lượng đó, ta có: \(\frac{1}{2}CU^2_0=\frac{1}{2}LI^2_0\)
Mà: \(^{U=\frac{U_0}{\sqrt{2}}}_{I=I_{\frac{0}{\sqrt{2}}}}\)} \(\rightarrow I^2=\frac{C}{L}.U^2\)
\(P=I^2R=\frac{CR}{L}U^2=\frac{CRU^2_0}{2L}\)
\(\Rightarrow P=137\mu W\)
chọn B


Đáp án B
Khi 3 phần tử mắc vào điện áp xoay chiều:
Khi mắc 3 phần tử này cho mạch cùng dao động thì do năng lượng tiêu tốn là do điện trở, do đó ta cần cung cấp một công suất lớn nhất tương ứng là Pcc