Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn trục căn thức ở mẫu rồi trừ đi là xong nhé,vì khi trục căn thức thì ở A mẫu chung là 1,ở B mẫu chung là 2.

\(\sqrt{\frac{5+2\sqrt{6}}{5-2\sqrt{6}}}+\sqrt{\frac{5-2\sqrt{6}}{5+2\sqrt{6}}}=\sqrt{\frac{\left(\sqrt{2}+\sqrt{3}\right)^2}{\left(\sqrt{3}-\sqrt{2}\right)^2}}+\sqrt{\frac{\left(\sqrt{3}-\sqrt{2}\right)^2}{\left(\sqrt{3}+\sqrt{2}\right)^2}}\)
\(=\frac{\sqrt{2}+\sqrt{3}}{\sqrt{3}-\sqrt{2}}+\frac{\sqrt{3}-\sqrt{2}}{\sqrt{2}+\sqrt{3}}=\frac{\left(\sqrt{2}+\sqrt{3}\right)^2+\left(\sqrt{3}-\sqrt{2}\right)^2}{\left(\sqrt{3}-\sqrt{2}\right)\left(\sqrt{3}+\sqrt{2}\right)}=\frac{5+2\sqrt{6}+\left(5-2\sqrt{6}\right)}{3-2}=10\)

\(\left(\frac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\frac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}=\left(\frac{\sqrt{7}\left(\sqrt{2}-1\right)}{1-\sqrt{2}}+\frac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}=\left(\frac{-\sqrt{7}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}+\frac{-\sqrt{5}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}=\left(-\sqrt{7}-\sqrt{5}\right):\frac{1}{\sqrt{7}-\sqrt{5}}=\frac{\sqrt{5}-\sqrt{7}}{\sqrt{7}+\sqrt{5}}=\frac{\left(\sqrt{5}-\sqrt{7}\right)\left(\sqrt{5}+\sqrt{7}\right)}{\left(\sqrt{7}+\sqrt{5}\right)^2}=\frac{2}{12+2\sqrt{35}}\)
\(\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}+\frac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}-\frac{\sqrt{5}+1}{\sqrt{5}-1}=\frac{\left(\sqrt{5}-\sqrt{3}\right)^2}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}+\frac{\left(\sqrt{5}+\sqrt{3}\right)^2}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+3\right)}-\frac{\sqrt{5}+1}{\sqrt{5}-1}=\frac{8-2\sqrt{15}}{2}+\frac{8+2\sqrt{15}}{2}-\frac{\left(\sqrt{5}+1\right)^2}{4}=8-\frac{6+2\sqrt{5}}{4}=\frac{26-2\sqrt{5}}{4}\)
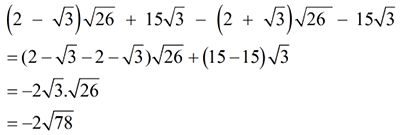

\(\left(\frac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\frac{5-\sqrt{5}}{1-\sqrt{5}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}.\)
\(=\left(\frac{\sqrt{7}\left(\sqrt{2}-1\right)}{1-\sqrt{2}}+\frac{\sqrt{5}\left(\sqrt{5}-1\right)}{1-\sqrt{5}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}.\)
\(=\left(\frac{-\sqrt{7}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}+\frac{-\sqrt{5}\left(1-\sqrt{5}\right)}{1-\sqrt{5}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}.\)
\(=\left(\left(-\sqrt{7}\right)+\left(-\sqrt{5}\right)\right)\cdot\frac{\sqrt{7}-\sqrt{7}}{1}\)
\(=-\left(\sqrt{7}+\sqrt{5}\right)\cdot\frac{\sqrt{7}-\sqrt{5}}{1}\)
\(=\frac{-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)}{1}\)
\(=\frac{-\left(7-5\right)}{1}=-2\)