Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D.
Phương trình tổng quát của đường thẳng Δ đi qua điểm M(-1;2) và có hệ số góc k = 3 là: y = 3(x + 1) + 2 ⇔ 3x - y + 5 = 0
Phương trình của ∆ là : y + 8 = -3(x + 5) <=> 3x + y + 23 = 0
a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6
a,\(\Delta_a\) : 3 (x-1) - 2 (y-1) =3x-2y-1=0
b, \(\Delta_b\) : y=-\(\dfrac{1}{2}\)(x-2) =-\(\dfrac{1}{2}\)x =>\(\Delta_b\) : x+2y=0
c,\(\overrightarrow{AB}\)=(-2;-3) =>vtpt \(\overrightarrow{n}\)=(3;-2)
=>\(\Delta_c\): 3 (x-2) - 2(y-0) =0
=>\(\Delta_c\): 3x-2y-6=0
Lời giải
a) \(\Delta_a=3\left(x-1\right)-2\left(y-1\right)=3x-2y+5=0\)
b)\(\Delta_b:y=-\dfrac{1}{2}\left(x-2\right)-1=-\dfrac{1}{2}x\Rightarrow\Delta_b:x+2y=0\)
c) \(\Delta_c:\left(3+0\right)\left(x-2\right)+\left(0-2\right)\left(y-0\right)=3x-2y-6\)
Đường thẳng ∆ đi qua A(2; 1) và B(-4; 5) nhận vectơ = (=6; 4) là một vectơ chỉ phương
Phương trình tham số của ∆ :
∆ :
Khử t giữa hai phương trình ta được phương trình tổng quát:
∆ : 2x + 3y – 7 = 0
a) Phương trình đường thẳng Δ đi qua M(–5; –8) và có hệ số góc k = –3 là:
y = –3.(x + 5) – 8 ⇔ 3x + y + 23 = 0.
b) Ta có: A(2; 1), B(–4; 5) ⇒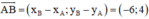
Δ đi qua hai điểm A(2; 1) và B(–4; 5)
⇒ Δ nhận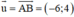
là một vtcp
⇒ Δ nhận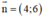
là một vtpt.
Phương trình tổng quát của đường thẳng Δ là:
(Δ) : 4(x – 2) + 6(y -1) = 0
Hay 4x + 6y – 14 = 0 ⇔ 2x + 3y – 7 = 0.