Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Khi đổ dần nước vào ống nghiệm đến độ cao 30cm thì thấy âm được khuyếch đại rất mạnh, có nghĩa là khi đó hiện tượng sóng dừng xảy ra, âm nghe được to nhất do tại đáy ống hình thành một nút sóng, miệng ống hình thành một bụng sóng. Mặt khác, nước cao 30cm thì cột không khí cao 50cm. Từ đó ta có:
\(300\left(\frac{1}{4.850+k\frac{1}{2.850}}\right)\le0,5=\)\(\frac{\lambda}{4}+k\frac{\lambda}{2}=v\left(\frac{1}{4f}+k\frac{1}{2f}\right)\le350\left(\frac{1}{4.850}\right)\)\(\Rightarrow1,93\le k\le2,33\Rightarrow k=2\)
\(\Rightarrow v=\frac{0,5}{\frac{1}{4.850+2.\frac{1}{2.850}}}=340\)
Từ đó dễ thấy \(\lambda\) = 40cm
Khi tiếp tục đổ nước vào ống thì chiều dài cột kí giảm dần, và để âm khuyếch đại mạnh thì chiều dài cột khí phải thỏa mãn
\(0< l=\frac{\lambda}{4}+k\frac{\lambda}{2}=10+k.20< 50\)
\(-0,5< k< 2\)
k = 0;1
Vậy khi đổ thêm nước vào thì có thêm 2 vị trí làm cho âm khuyếch đại rất mạnh
chọn A
Trước tiên ta thấy rằng trong ống lúc đổ nước và đến độ cao 30cm thì có sóng dừng giống sợi dây 1 đầu cố định, 1 đầu tự do.
Vậy ta có : \(l=\left(2k+1\right)\lambda\Rightarrow\lambda=\frac{4l}{\left(2k+1\right)}\) (2)
Mặt khác ta có: \(v=\lambda f\) (1)
Từ (1) và (2) ta có:
\(v=\frac{4lf}{2k+1}=\frac{4\left(0,8-0,3\right)850}{2k+1}=\frac{1700}{2k+1}\)
Vì vận tốc truyền âm nằm trong khoảng:
\(300\le v\le500\Rightarrow300\le\frac{1700}{2k+1}\le350\Rightarrow1,9\le k\le2,3\Rightarrow k=2\)
Vậy vận tốc truyền âm và bước sóng của âm là:
\(v=\frac{1700}{2.2+1}=340\left(\frac{m}{s}\right)\Rightarrow\lambda=\frac{v}{f}=0,4m=40cm\)
Như vậy tính cả miệng ống thì có 3 bụng sóng. Vì:
\(l=\left(2n+1\right)\frac{\lambda}{4}\Rightarrow\pi=\frac{4.50}{2.40}-0,5=2\)
N = 2+1=3 Vậy sẽ có 3 vị trí.
Vậy B đúng
nso2 =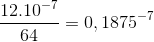 
(mol)
Nồng độ mol/m3 SO2 của thành phố là:
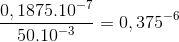(mol/m3)
So với tiêu chuẩn quy định, lượng SO2 chưa vượt quá, không khí ở đó không bị ô nhiễm.
\(P=UI\cos\varphi\)
=> \(I=\frac{P}{U\cos\varphi}=\frac{P_i+I^2r}{U\cos\varphi}=\frac{80+I^2.32}{220.0.8}\)
=> phương trình bậc 2 của I và bấm máy tính
\(I_1=5\)(loại vì hiệu suất \(H=\frac{80}{UI\cos\varphi}=9,09\%\))
hoặc \(I_2=0.5\) (chọn)
=> \(I_0=I\sqrt{2}=0,5\sqrt{2}A.\)
chọn đáp án D.
Bạn tham khảo một bài tương tự ở đây nhé.
Câu hỏi của trần thị phương thảo - Học và thi online với HOC24
Khi phát ra tia Rơn ghen thì động năng của e chuyển thành năng lượng tia X
\(\Rightarrow W_đ=hf\)
Cường độ dòng điện: \(I=n_e.1,6.10^-19\), suy ra \(n_e\)
\(\Rightarrow \) Nhiệt lượng làm nóng Katot: \(Q=0,999.n_e.hf\)
\(Q=m.c.\Delta t \Rightarrow m \Rightarrow V\)