Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\widehat{BOx}=\widehat{B}\left(=50\text{°}\right)\)
mà \(\widehat{BOx}\) và \(\widehat{B}\) là 2 góc SLT
\(\Rightarrow Ox\text{∥}BC\) (dấu hiệu nhận biết 2 đường thẳng song song)
b) \(\widehat{BAC}+\widehat{OAC}=180\text{°}\) (2 góc kề bù)
Thay số: \(80\text{°}+\widehat{OAC}=180\text{°}\)
\(\widehat{OAC}=100\text{°}\)
AI là tia phân giác của \(\widehat{OAC}\) (giả thiết)
\(\Rightarrow\widehat{OAI}=100\text{°}\div2=50\text{°}\)
\(\Rightarrow\widehat{OAI}=\widehat{B}\left(=50\text{°}\right)\)
mà \(\widehat{OAI}\) và \(\widehat{B}\) là 2 góc đồng vị
\(\Rightarrow AI\text{∥}BC\) (dấu hiệu nhận biết 2 đường thẳng song song)

Hình tự vẽ
a. Vi DÂB và BÂC kề bù nên:
DÂB + BÂC = 180
DÂB + 80 = 180
=> DÂB = 180 - 80 = 100
Vì AM là tia phân giác của DÂB nên:
DÂM = BÂM = DÂB/2 = 100/2 = 50
=> DÂM = ADE = 50 mà hai góc này ở vị trí so le trong
=> DE // AM (đpcm)
b. Ta có D = C và hai góc này ở vị tró so le trong (GT)
=> DE // BC
Mà DE // AM ( câu a )
=> DE // BC // AM
=> BC // AM (đpcm )
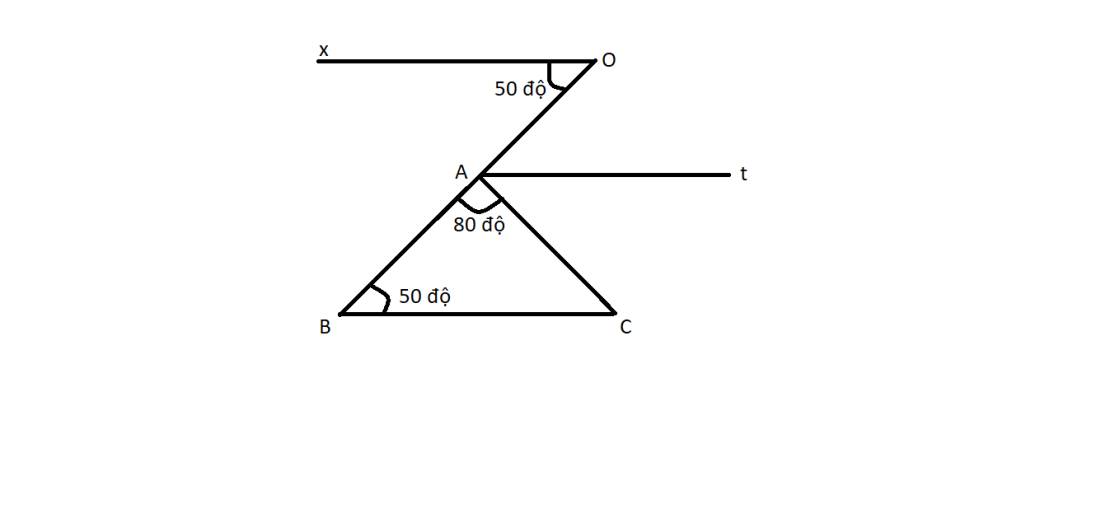
a:
Xét ΔABC có góc OAC là góc ngoài tại đỉnh A
nên \(\widehat{OAC}+\widehat{BAC}=180^0\)
=>\(\widehat{OAC}=180^0-80^0=100^0\)
At là phân giác của góc OAC
=>\(\widehat{tAO}=\widehat{tAC}=\dfrac{\widehat{OAC}}{2}=\dfrac{100^0}{2}=50^0\)
\(\widehat{tAO}=\widehat{CBA}\)(=50 độ)
mà hai góc này là hai góc ở vị trí đồng vị
nên At//BC
\(\widehat{xOA}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Ox//BC
b:
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+80^0+50^0=180^0\)
=>\(\widehat{ACB}=50^0\)