K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 1 2024
a.
\(A=\left(\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}+\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-2\right)}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+x+1}{x}+\dfrac{x+2}{x}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+3x+1}{x}\right).\dfrac{x}{x+1}\)
\(=\dfrac{x^2+3x+1}{x+1}\)
2.
\(x^3-4x^3+3x=0\Leftrightarrow x\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=1\left(loại\right)\\x=3\end{matrix}\right.\)
Với \(x=3\Rightarrow A=\dfrac{3^2+3.3+1}{3+1}=\dfrac{19}{4}\)
AH
Akai Haruma
Giáo viên
3 tháng 2 2024
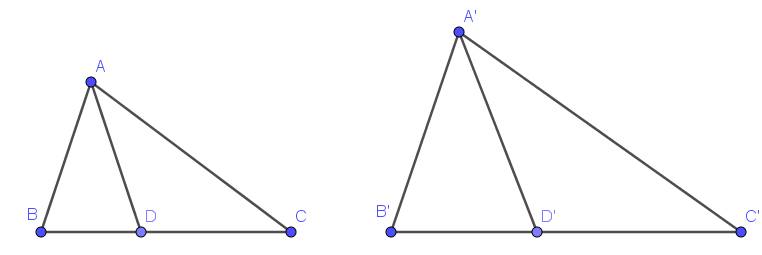
Bài 4:
a. Vì $\triangle ABC\sim \triangle A'B'C'$ nên:
$\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}(1)$ và $\widehat{ABC}=\widehat{A'B'C'}$
$\frac{DB}{DC}=\frac{D'B'}{D'C}$
$\Rightarrow \frac{BD}{BC}=\frac{D'B'}{B'C'}$
$\Rightarrow \frac{BD}{B'D'}=\frac{BC}{B'C'}(2)$
Từ $(1); (2)\Rightarrow \frac{BD}{B'D'}=\frac{BC}{B'C'}=\frac{AB}{A'B'}$
Xét tam giác $ABD$ và $A'B'D'$ có:
$\widehat{ABD}=\widehat{ABC}=\widehat{A'B'C'}=\widehat{A'B'D'}$
$\frac{AB}{A'B'}=\frac{BD}{B'D'}$
$\Rightarrow \triangle ABD\sim \triangle A'B'D'$ (c.g.c)
b.
Từ tam giác đồng dạng phần a và (1) suy ra:
$\frac{AD}{A'D'}=\frac{AB}{A'B'}=\frac{BC}{B'C'}$
$\Rightarrow AD.B'C'=BC.A'D'$
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2023
Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\Rightarrow xyz=1\) và \(x;y;z>0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P=\dfrac{1}{\dfrac{1}{x^3}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)}+\dfrac{1}{\dfrac{1}{y^3}\left(\dfrac{1}{z}+\dfrac{1}{x}\right)}+\dfrac{1}{\dfrac{1}{z^3}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}\)
\(=\dfrac{x^3yz}{y+z}+\dfrac{y^3zx}{z+x}+\dfrac{z^3xy}{x+y}=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
\(P\ge\dfrac{\left(x+y+z\right)^2}{y+z+z+x+x+y}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
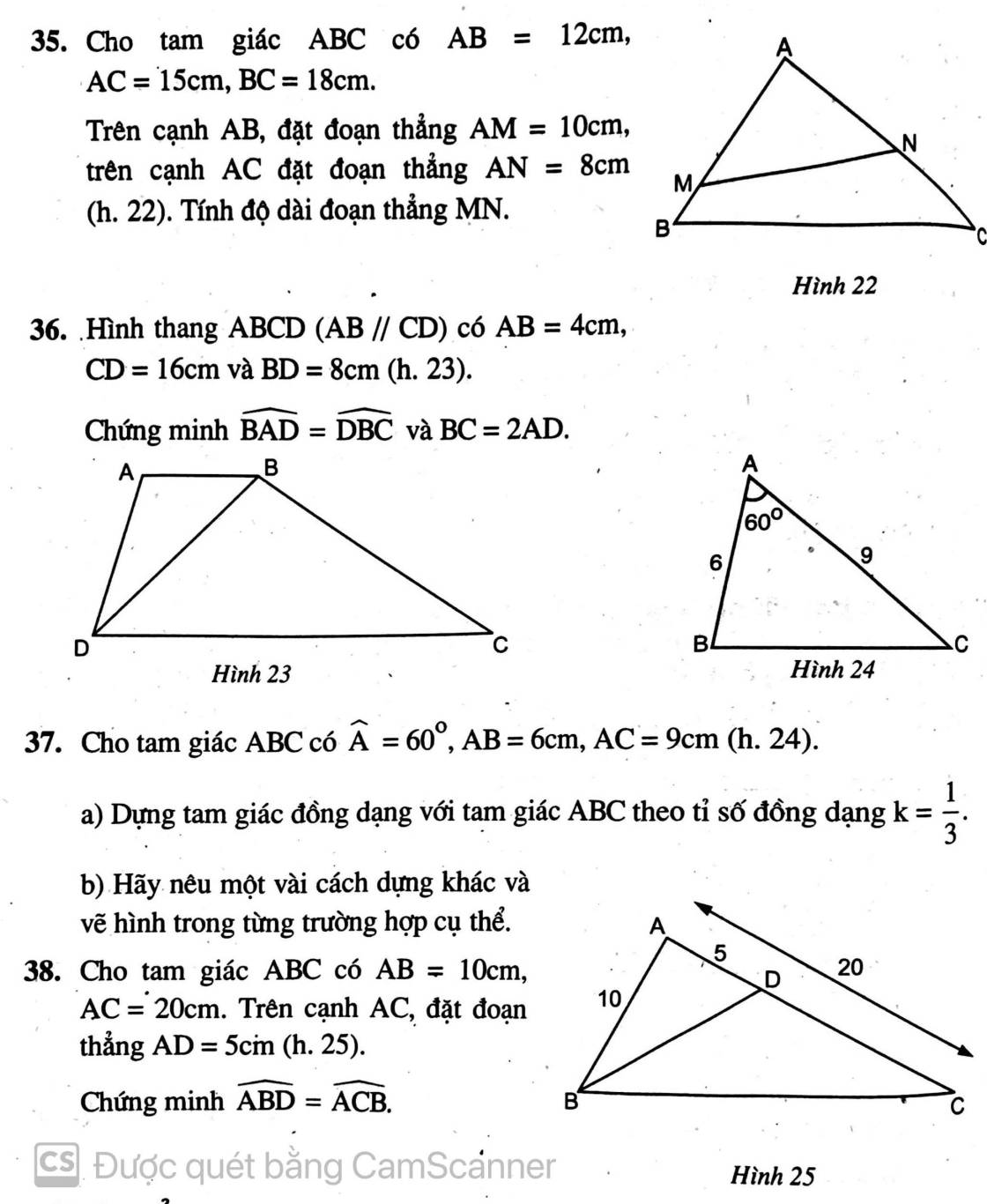
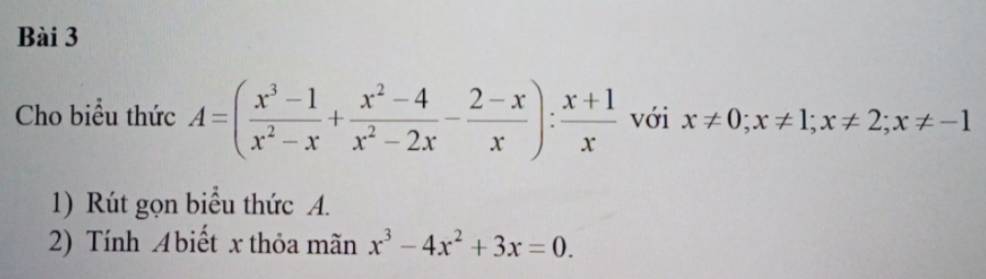
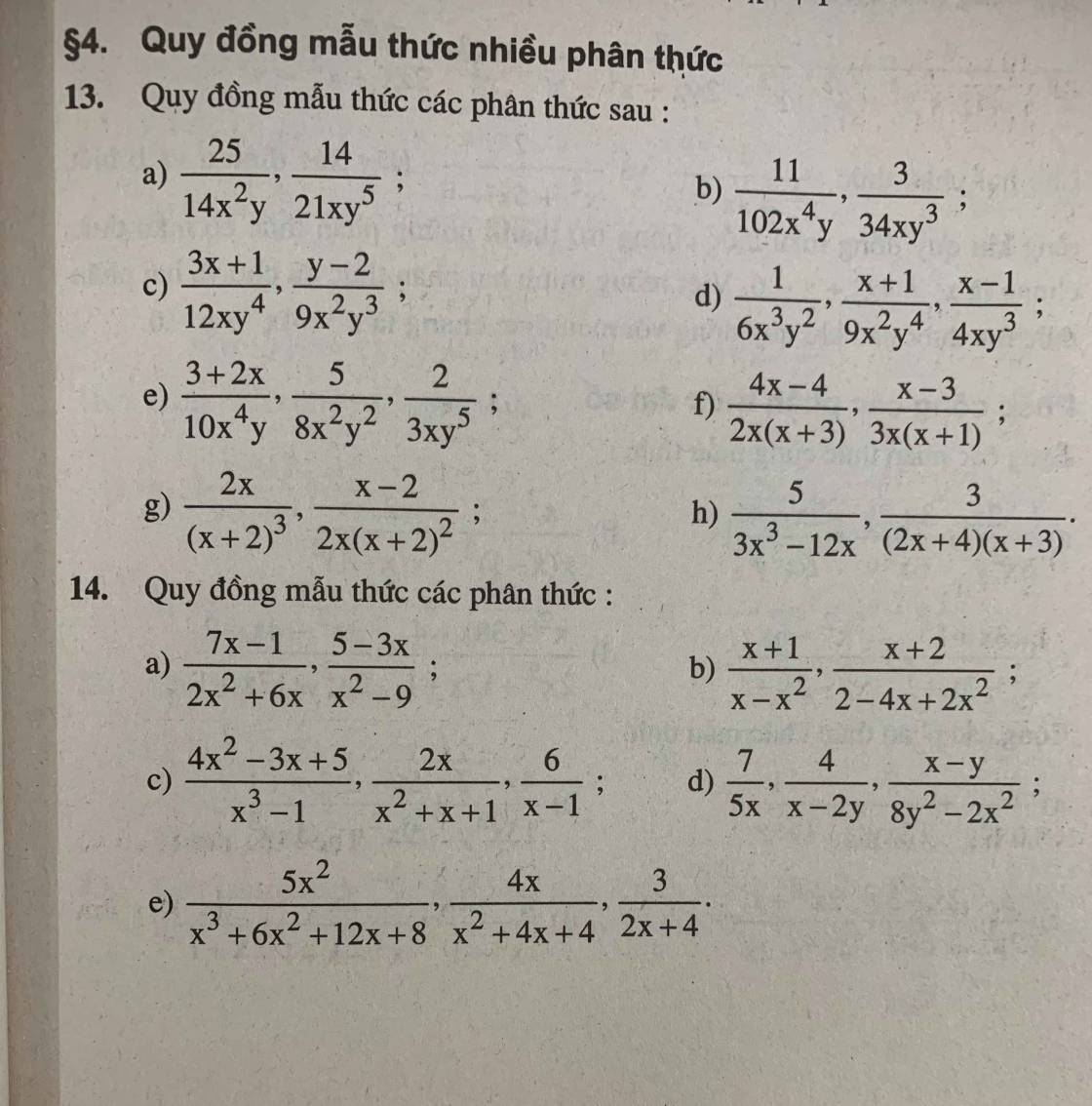
Cách làm chung của các bài từ 1 đến 7 là từ điều kiện đã cho, tính ẩn này theo ẩn kia (hạn chế phân số) rồi thay vào biểu thức cần tìm min (max) rồi quay về dạng toán tìm min (max) của đa thức bậc 2 quen thuộc. Mình mẫu 1 câu nhé:
1. Tìm min của \(A=3x^2+y^2\) biết \(3x+y=1\)
Ta có \(3x+y=1\Leftrightarrow y=1-3x\) (hoặc bạn có thể suy ra \(x=\dfrac{1-y}{3}\) nhưng làm như thế khi thay vào biểu thức A sẽ gặp khó khăn)
Thế \(y=1-3x\) vào A, ta được \(3x^2+\left(1-3x\right)^2=3x^2+1-6x+9x^2=12x^2-6x+1\)
Tới đây việc tìm min của A chắc mình không cần làm nữa đâu nhỉ?
Ở bài 8 và 9, việc rút ẩn này theo ẩn kia rồi thay vào sẽ gây khó khăn vì các biến nằm ở dưới mẫu khá khó xét. Để ý rằng giả thiết cho \(a,b>0\), hơn nữa các biến còn có vai trò như nhau trong biểu thức cần tìm min (max) nên ở dạng bài này, ta hay có trò sử dụng các BĐT như Cô-si, Bu-nhi-a-cốp-xki,... Ví dụ:
8. Cho \(a,b>0\) và \(a+b=4\). Tìm max của \(P=\left(1-\dfrac{1}{a}\right)\left(1-\dfrac{1}{b}\right)\).
Ta thấy \(P=1-\left(\dfrac{1}{a}+\dfrac{1}{b}\right)+\dfrac{1}{ab}=1-\dfrac{a+b}{ab}+\dfrac{1}{ab}\) \(=1-\dfrac{4}{ab}+\dfrac{1}{ab}\) \(=1-\dfrac{3}{ab}\). Ta lại có \(ab\le\dfrac{\left(a+b\right)^2}{4}=4\) nên \(\dfrac{3}{ab}\ge\dfrac{3}{4}\) hay \(P=1-\dfrac{3}{ab}\le1-\dfrac{3}{4}=\dfrac{1}{4}\). Dấu "=" xảy ra \(\Leftrightarrow a=b=2\).
Riêng câu số 5 mình nhấn mạnh một chút, vì các biến trong biểu thức đã cho có bậc 3 nhưng các biến đối xứng kiểu như thế thì ta sẽ tìm cách đưa về tổng và tích:
\(C=x^3+y^3+xy=\left(x+y\right)^3-3xy\left(x+y\right)+xy\) \(=1-3xy+xy=1-2xy\)
rồi làm như bình thường.