Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Bản phẳng coi như gồm hai bản AHEF và HBCD ghép lại.
Biểu diễn trọng tâm các bản như hình vẽ sau:
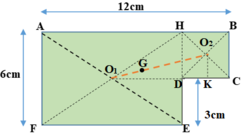
Vì các bản đồng chất, phẳng mỏng đều nên tỉ lệ diện tích bằng tỉ lệ về trọng lượng:
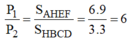
Gọi G là trọng tâm của cả bản phẳng => G phải nằm trền đoạn thẳng O 1 O 2 , trong đó O 1 là trọng tâm của bản AHEF, O 2 là trọng tâm của bản HBCD.
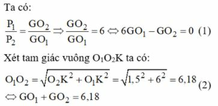
Giải hệ (1) và (2) ta được: O G 1 = 0,88 c m
Vậy trọng tâm G của bản phẳng nằm trên đoạn O 1 O 2 cách O 1 một đoạn 0,88 cm.

Bản phẳng coi như gồm hai bản AHEF và HBCD ghép lại.
Biểu diễn trọng tâm các bản như hình vẽ sau:
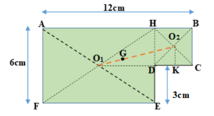
Vì các bản đồng chất, phẳng mỏng đều nên tỉ lệ diện tích bằng tỉ lệ về trọng lượng:
![]()
Gọi G là trọng tâm của cả bản phẳng ⇒ G phải nằm trền đoạn thẳng O1O2, trong đó O1 là trọng tâm của bản AHEF, O2 là trọng tâm của bản HBCD.
Ta có:
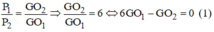
Xét tam giác vuông O1O2K ta có:
![]()
Giải hệ (1) và (2) ta được: GG1 ≈ 0,88 cm
Vậy trọng tâm G của bản phẳng nằm trên đoạn O1O2 cách O1 một đoạn 0,88 cm.

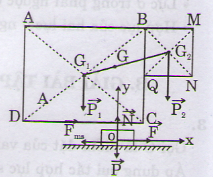
Chia bản mỏng thành hai phần.
ABCD và BMNQ. Trọng tâm của 2 phần này là G1 và G2. Nếu gọi trọng tâm của bản lề G thì G sẽ là điểm đặt của hợp lực của các trọng lực P1 và P2 của hai bản nói trên.
Do trọng lượng của mỗi tấm tỉ lệ với diện tích.
Ta có: =
=
= 6
Khi đó G được xác định như sau:
=
= 6 (1)
Mặt khác ta có: G1G2 = = 6,18 cm
=> GG1 + GG2 = 6,18 (2)
(1)và(2) => GG1 = 0,882 cm
Vậy trọng tâm G nằm trên đường nối G1 và G2; cách G1 một đoạn 0,882cm

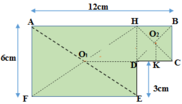
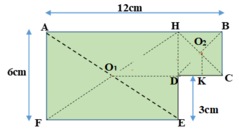
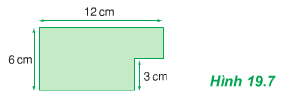
Vì bản phẳng, mỏng, đồng chất nên ta có thể coi nó gồm hai tấm ghép lại.
- Tấm thứ nhất có dạng hình chữ nhật, dài $9 cm$, rộng $6 cm$; trọng lực là $\overrightarrow{P}_1$ đặt tại $G_1$
- Tấm thứ hai có dạng hình vuông, mỗi cạnh $3cm$; trọng lực là $\overrightarrow{P}_2$ đặt tại $G_2$.
Như vậy bản phẳng cần xét có trọng lực là $\overrightarrow{P}=\overrightarrow{P}_1+\overrightarrow{P}_2$ và đặt tại $G$.
Theo quy tắc hợp lực song song: $\frac{P_1}{P_2}=\frac{d_2}{d_1}=\frac{GG_2}{GG_1}$
Mặt khác: $\frac{P_1}{P_2}=\frac{S_1}{S_2}=\frac{6.9}{3.3}=6\Rightarrow GG_2=6.GG_1 (1)$
Dựa vào hình vẽ ta có: $G_1G_2=\sqrt{6^2+1,5^2}=6,18cm (2)$
Từ $(1)$ và $(2)$, suy ra $GG_1=0,88 cm$
Vậy vị trí của $G$ nằm trong khoảng $G_1G_2$ và cách $G-1$ là $0,88 cm$

Để đoạn dây đồng ab cân bằng ta phải có :
P = F
↔ P = 2 . σ . ab = 2 . 4 .10-2 . 5 .10-2
= 40 . 10-4 N = 4 . 10-3 N
Vậy để đoạn dây ab cân bằng ta phải có trọng lượng P = 4 . 10-3 N.
@phynit
Em trả lời 100% . Không có sự tự hỏi tự trả lời đâu ạ ( Em nói để thầy biết và không nghĩ oan cho em )

Để đoạn dây đồng ab cân bằng ta phải có :
P = F
↔ P = 2 . \(\sigma\). ab = 2 . 4 .10-2 . 5 .10-2
= 40 . 10-4 N = 4 . 10-3 N
Vậy để đoạn dây ab cân bằng ta phải có trọng lượng P = 4 . 10-3 N.

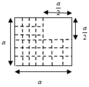
Áp dụng phương pháp tọa độ :
x G = y G = m a 4 + m a 4 + m 3 a 4 3 m = 5 a 12
Chọn A.
Bản phẳng coi như gồm hai bản AHEF và HBCD ghép lại.
Biểu diễn trọng tâm các bản như hình vẽ sau:
Vì các bản đồng chất, phẳng mỏng đều nên tỉ lệ diện tích bằng tỉ lệ về trọng lượng:
Gọi G là trọng tâm của cả bản phẳng => G phải nằm trền đoạn thẳng O1O2, trong đó O1 là trọng tâm của bản AHEF, O2 là trọng tâm của bản HBCD.
Ta có:
Xét tam giác vuông O1O2K ta có:
Giải hệ (1) và (2) ta được: GG1 0,88 cm
Vậy trọng tâm G của bản phẳng nằm trên đoạn O1O2 cách O1 một đoạn 0,88 cm.